शून्य, आकार आणि अनंताची वाटचाल

हे चित्र पाहा. तुम्ही म्हणाल या चित्र काय , दोन बिंदू तर आहेत. ठीक तर. मग असं म्हणतो की ’A आणि B हे दोन बिंदू पाहा.’ ’प्रत्येक बिंदू हा बिंदू स्वयंभू असतो ’ हे आपण भूमितीमध्ये फार वर्षांपूर्वी शिकलो. तो शून्य मिती, शून्य लांबी व क्षेत्रफळ असलेला मानलेला आहे. (असल्या सुरुवातीनंतर गणित अप्रिय झाले नाही तरच नवल. :) )

आता माझ्याकडे एक नव्हे, दोन बिंदू आहेत. आता यांच्याबद्दल एकत्रितपणे काय म्हणता येईल? मग ’दोन भिन्न बिंदूंतून एक आणि एकच रेषा जाते’ हा पुढच्या सिद्धांत आपल्याला आठवेल. तर हे घ्या, दोन बिंदूंना जोडून मी ही रेषा- रेषाखंड A-B मी तयार केला.

आता मी द्विमितीमध्ये* प्रवेश केला आहे. आता द्विमितीमध्ये मला फक्त रेषाखंडच नव्हे तर इतर अनेक आकार माहित आहेत. या दोन बिंदूंसाठी त्यापैकी एखादा आकार योग्य ठरेल का? बहुतेकांच्या मनात येईल की दोन बिंदू असतील तर फक्त एक रेषाच असू शकते ना? त्रिकोणाला तीन बिंदू लागतात नि चौकोनाला चार...

जर तुम्ही असा विचार करत असाल तर तो चुकीचा आहे! तुमची पंचाईत अशी आहे की तुम्ही बिंदू जोडण्याच्याच संदर्भात विचार करत आहात. मुळात त्रिकोण आणि चौकोन यांच्यामध्ये तीन आणि चार नव्हे तर अनंत बिंदू असतात. कारण या आकृत्या रेषाखंडांनी बांधलेल्या आहेत, आणि प्रत्येक रेषाखंड ही अनंत बिंदूंची साखळी आहे. आता पुढचा प्रश्न विचारतो. 'हे दोन बिंदू कोणत्या आकृतीचे आहेत?' काहींच्या मनात उत्तर उमटेल, एका रेषेचे. हे पुन्हा चूक आहे. कारण रेषाखंड ही आकृती तुमच्यासमोर की आधीच काढून ठेवली आहे म्हणून तुम्हाला दिसते आहे. पण द्विमितीय प्रतलात याहून अनेक अदृश्य आकृत्या असतील ज्याचे केवळ हे दोनच बिंदू तुम्हाला दिसत असतील तर...

आता ही पुढची आकृती पाहा.

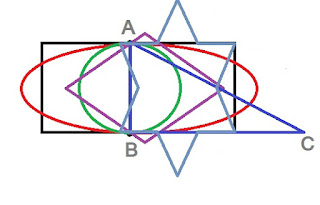
आता तुम्हाला दिसेल एक आयत (काळा) एक चौकोन (जांभळा), एक वर्तुळ (हिरवे), एक लंबवर्तुळ (लाल), एक त्रिकोण (निळा) आणि एक द्वादशकोन अर्थात चांदणी (फिकी निळी) इतके आकार दिसतील. या सार्‍यांचे वैशिष्ट्य असे की या त्या रेषाखंडाची टोके असणारे ते दोन बिंदू या सार्‍यांच्याच परिघावर आहेत. हे दोन बिंदू या सार्‍याच आकृत्यांचा भाग आहेत.

यातील चौकोन, त्रिकोण आणि चांदणी यांचे रेषाखंडाभोवती यांचे प्रतिबिंब घेतले तर आणखी एक चौकोन, त्रिकोण, चांदणी मिळेल, ज्यांच्या परिघावर A आणि B हे दोनही बिंदू असतील. मधल्या लंबवर्तुळाचा एक अक्ष (उभा) A-B हाच ठेवून दुसर्‍या (आडव्या) अक्षाची लांबी वाढवून वा कमी करुन आणखी लंबवर्तुळे मिळतील. A आणि B हे बिंदू यांच्याही परिघावर असतील.

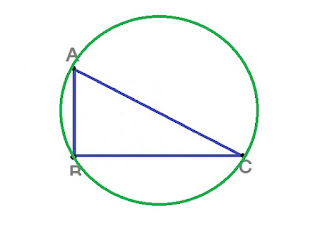
त्यामुळे नुसते ते दोन बिंदू दिले, आणि ’मूळ आकृती ओळखा’ म्हटले तर असंख्य पर्याय आहेत. आता मी एक पाऊल पुढे टाकून C हा तिसरा बिंदूही दिला आणि तोच प्रश्न विचारला तर? काही जणांचे उत्तर येईल त्रिकोण... आणि ते दोन बिंदूंसाठी ’रेषाखंड’ या उत्तराइतकेच चूक असेल! कारण आताही तुम्ही केवळ तुमच्यासमोरील पर्यायांतून निवडत आहात. तुमच्यासमोर न दिसणार्‍या इतर अनेक आकृत्यांच्या परिघावर हे तीन बिंदू असू शकतील.

सर्वात सोपे उदाहरण म्हणजे या तीन बिंदूंतून जाणारे, आणि हा त्रिकोण पूर्णपणे पोटात घेणारे, एखादे वर्तुळ मी काढून दाखवू शकेन. किंवा निळ्या त्रिकोणाचे त्याच्या कर्णापाशी प्रतिबिंब घेऊन तयार होणारा त्रिकोण त्या कर्णापाशीच जोडून एक आयत तयार होईल. आता माझ्याकडे तीन पर्याय झाले. हाच आयत लांबीच्या बाजूला आणखी ताणून अनेक आयत मिळतील. आता हे तीन बिंदू त्याच्या कोपर्‍याशी नव्हे तर बाजूंच्या अधेमध्ये येतील. थोडक्यात मला अशा अनेक आकृत्या काढता येतील ज्यांच्या परिघावर हे तीन बिंदू असतील.

इथे एक महत्त्वाचा मुद्दा नोंदवून ठेवला पाहिजे. आपल्या समोर असलेले तीन बिंदू सांधणारा रेषाखंड आपल्याला उपलब्ध नाही. त्यामुळे या तीनही बिंदूंना सांधणार्‍या संभाव्य आकृतींच्या सूचीमधून रेषाखंड ही आकृती बाद करावी लागणार आहे.

प्रत्येक वेळी नवा बिंदू समाविष्ट झाला की काही संभाव्य आकृत्यांना तो बाद करत नेईल. यातून उपलब्ध बिंदूंच्या संचाला सामावून घेतील अशा आकृत्यांची सूची हळूहळू आक्रसत जात असते.

जर आपला समज असा असेल की आपल्यासमोर येणार्‍या - आधीच आलेल्या वा भविष्यात येणार्‍या - बिंदूंच्या संचांना सामावून घेईल अशी ’एक आणि एकच’ अशी आकृती आहे, तर नव्याने उपलब्ध झालेल्या प्रत्येक बिंदूमुळे आक्रसत गेलेल्या सूचीमध्ये पुरेसे बिंदू जमा झाल्यावर ती देव-आकृतीच शिल्लक राहील असे म्हणता येईल का? यासाठी ’पुरेसे म्हणजे किती बिंदू?’ या प्रश्नाचे उत्तर हे आधीच समाविष्ट झालेल्या बिंदूंवर अवलंबून राहील (उदा. C हा तिसरा बिंदू A-B रेषेवरच असेल तर तो संभाव्य आकृतींच्या सूचीतून रेषाखंड बाद करणार नाही.)

वास्तविक आयुष्यात अशी एक आणि एकच आकृती शिल्लक राहावी इतके बिंदू जमा होतच नसतात. आणि समजा, ती संख्या ठाऊक झाली, तरी तेवढे जमा करण्यास गुंतवावी लागणारी ऊर्जा व आर्थिक ताकद अमर्याद वेगाने वाढते. माणसाला कुठेतरी थांबावे लागते. त्या थांब्याच्या क्षणी उपलब्ध असणार्‍या बिंदूंतून सर्वाधिक संभाव्य(probable) आकृती निवडावी लागते. आणि तिच्यापासून आपण किती दूर असू शकतो याचा अदमासही (variance) घ्यावा लागतो.

पण इथेच न थांबता मी जर पुढच्या- म्हणजे तिसर्‍या मितीमध्येही प्रवेश केला, तर ज्यांच्या परिघावर हे तीन बिंदू असतील अशा इतर अनेक आकृत्या तिथे मिळू शकतात.

’जोवर आकृती रेखाटली गेलेली नाही, तोवर ती अस्तित्वातच नाही. त्यामुळे हे दोन बिंदू तिचे भाग आहेत की नाही हा प्रश्नच उद्भवत नाही.’ असा विचार तुम्ही केला असला... तर तो बरोबर आहे! कारण त्या आकृतीचे अस्तित्वच तुमच्यामुळे आहे. तुम्ही तिला जन्म दिला आहे. त्यानंतरच तिच्या संदर्भात तुम्ही बोलू शकत आहात. थोडक्यात आकृतीचे अस्तित्व आपण गृहित धरू शकत नाही. ती दिसत (व्यापक अर्थाने तिचे अस्तित्व सिद्ध होत) असेल तरच तिचा नि आपल्याला दिलेल्या बिंदूंचा संबंध आपण तपासू शकतो.

वरच्या उदाहरणात म्हटले तसे दोन बिंदूंमध्ये तुम्हाला सर्वात सोपी नि सोयीची म्हणून रेषा- रेषाखंड ही आकृती समजून पुढे जाल. तुम्ही असा विचार करणार नाही, की जे बिंदू या दोघांशी संबंधित आहेत, पण मला अजून दिसलेले नाहीत, त्यांना सोबत घेतले तर कदाचित त्यांतून एक सरळ रेषा काढून दाखवता येणारही नाही. भूमितीत एकरेषीय म्हणतात तसेच हे सारे बिंदू असतील याची खात्री देण्यासाठी कोणतीही अधिक माहिती तुमच्याकडे नाही. त्यामुळे तूर्त रेषाखंड ही त्या दोघांना जोडणारी आकृती आहे असे समजणे सयुक्तिक असले, तरी तिसरा बिंदू सापडल्यावर हा समज रद्द होऊ शकतो आणि दुसरीच आकृती निवडावी लागू शकते’ ही शक्यता तुम्ही मान्य करून ठेवलेली असते. थोडक्यात रेषाखंड हे अंतिम सत्य नाही हे तुम्हाला मान्य करावे लागते.

तिसरा वा चौथा बिंदू सापडल्यावर त्या सार्‍यांना सोबत घेऊन एकत्रितपणे रेषाखंडापासून, त्रिकोण वा वर्तुळ यासारखे सारे पर्याय मला तपासावे लागतात. आता त्या तिघांचा परस्परसंबंध भौमितिकदृष्ट्या कसा आहे हे मला निश्चित सांगण्यासाठी वर्तुळ निवडावे की त्रिकोण यासाठी काही वस्तुनिष्ठ निकष आवश्यक ठरतात.

दोन बिंदूंना सामावणार्‍या सार्‍या आकृत्यांकडे पाहिले तर त्या दोन बिंदूंना जोडणारी, कमीतकमी परिमिती (लांबी) असणारी आकृती म्हणजे रेषाखंड होता. इथे मी परिमितीऐवजी मी क्षेत्रफळ हा निकष घेतला, तरी रेषाखंडच सर्वात कमी क्षेत्रफळाचा (शून्य) ठरतो. पण मी तिसर्‍या मितीमध्ये गेलो, तर आणखी काही मोजमापे मला उपलब्ध होतील. ज्यांच्या आधारे मला उपलब्ध असलेल्या, तोवर पाहता आलेल्या बिंदूंच्या आधारे एक आकृती निवडता येईल. निकष बदलला की निवड बदलेल हे ओघाने आलेच. या दोघांच्या सोबतीला तिसरा बिंदू (C) जेव्हा प्रवेश करेल तेव्हा त्यांना जोडणारे वर्तुळ वा त्रिकोण यांची परिमिती वा क्षेत्रफळ (मी जो निकष निवडला असेल तो) मोजून, जो कमी भरेल (किंवा जास्तही, पुन्हा तो माझा निर्णय) ती आकृती मी त्या तीन बिंदूंची प्रातिनिधिक म्हणून निवडेन. बिंदूंची संख्या जसजशी वाढत जाईल, तसतशी मी निवडलेली आकृतीही बदलत जाण्याची शक्यता बरीच आहे.

मानवी जिज्ञासा आणि त्यातून मानवाने सिद्ध केलेल्या ज्ञानाचे नातेही असेच आहे. माहितीमध्ये जसजशी भर पडत जाते, तसतसे मानवाचे आकलन आणि त्यातून त्याने सिद्ध केलेले ज्ञान हे वास्तव नावाचे काही असेलच (हा तत्त्वज्ञानाच्या मंडळींसाठी ठेवलेला चोरदरवाजा) तर त्याच्या अधिकाधिक जवळ पोहोचत जातो. परंतु त्यालाही आपल्याला उपलब्ध असणारे बिंदू, त्यांची संख्या, आपल्या मेंदूची विविध आकृत्या वेगळ्या ओळखण्याची कुवत, आपण निवडीसाठी निवडलेले निकष यांच्यासंदर्भातच आपली निवड सिद्ध होत असते. आणि असे नवनवीन बिंदू माणसाच्या जाणिवेच्या कक्षेत सतत प्रवेश करत असतात, माणसाला जुन्या आकलनाला आव्हान देण्यास उद्युक्त करत असतात. हा प्रवास अनंत काळ चालू राहतो कारण माहितीस्वरूप बिंदूंची संख्या अनंत आहे आणि माणसाची जिज्ञासा अमर्याद.

नमनाला भूमितीचे महागाचे घडाभर तेल ओतले असले तरी यातून जगण्यातील विषय नि मुद्द्यांचेही आकलन होत जाते असे मला म्हणायचे आहे. ’मला दिसणार्‍या बिंदूना सामावून घेणारी एक आणि एकच आकृती आहे, ती कुण्या आकाशातल्या बापाने आधीच बिनचूक निवडून ठेवली आहे... आणि ती अमुक एका पुस्तकात रेखाटून ठेवली आहे.’ हा अंधविश्वास माणसाला एकाच आकृतीशी बांधून ठेवतो. पुढे आणखी बिंदू दिसू लागले, माणसाच्या जाणिवेचे नि आकलनाचे क्षेत्र विस्तारत गेले, तरीही तो ’जुनी आकृती रद्द करुन दुसरी स्वीकारावी लागेल का?’ याचा विचार करणे बंद करतो. बर्‍याच काळापूर्वी मोजक्या बिंदूंच्या आधारे तयार झालेल्या आकृतीला, तुटपुंज्या माहितीवर सिद्ध झालेल्या ज्ञानाला, अंतिम समजून आपल्या जिज्ञासेची हत्या करतो. वैद्यकीय शास्त्रात मेंदूमृत ही संकल्पना आहे, त्या धर्तीवर ज्ञानक्षेत्रात यांच्यासाठी जिज्ञासामृत अशी संकल्पना मांडायला हवी. आपला वैचारिक मृत्यू मान्य करण्याऐवजी ही मंडळी ज्ञानालाच कुंपण घातल्याची अगोचर घोषणा करतात, जगण्याऐवजी जिवंत राहण्याचे मर्यादित साध्य स्वीकारतात.

- oOo -

*रेषा अथवा रेषाखंड हा स्वत: एकमितीय असतो, परंतु आपण तिला द्विमितीय (X-Y) कार्टेशिअन सिस्टमच्या संदर्भात अभ्यासत असतो.

(आता बिंदू हे डेटा पॉईंट्स अर्थात निरीक्षणे/मोजमापे आणि आकृती म्हणजे संख्याशास्त्रीय मॉडेल असा विचार केला तर हे सारे विवेचन भूमितीमधून अंकगणित-संख्याशास्त्राच्या क्षेत्रात जाईल. हा प्रवास त्याचा पूर्वरंग म्हणून झाला... जो मुळात माझ्या उत्क्रांतीबाबतच्या विवेचनाची तार्किक बैठक म्हणून मांडत होतो. या दोन्हींबद्दल पुन्हा केव्हातरी.)

माझी ब्लॉगयात्रा - ८ : केल्याने प्रसिद्धी

माझी ब्लॉगयात्रा - ७ : मोबाईल-विशेष << मागील भाग
---

इतरांकडून शिकावे

आपल्या लेखनाची, ब्लॉगची, वेबसाईटची जाहिरात कशा तर्‍हेने करावी, वाचकांना कसे खेचून आणावे, त्यांना पकडून कसे ठेवावे, याची उदाहरणे विविध वेबसाईट्सवर दिसत असतात. बारकाईने लक्ष दिले तर, आपणही ती वापरु शकतो का, आपल्या ब्लॉगसाठी ती उपयुक्त ठरु शकतात का, याची चाचपणी करुन पाहता येते.

एक 'केस-स्टडी' म्हणून maharashtratimes.com वेबसाईट पाहता येईल. वेबसाईट ओपन केल्यावर सर्वात वरच्या बाजूला महाराष्ट्र टाईम्सच्या लोगोच्या बरोबर खाली ’ट्रेडिंग’ची पट्टी दिसते. पॉप्युलर- म्हणजे सर्वाधिक वाचल्या जाणार्‍या लेखांकडे जाण्यासाठी वाचकाला दिलेला शॉर्टकट आहे. त्याच्या विरुद्ध दिशेला उजवीकडे वर ’रीड अ‍ॅंड अर्न’ची (Read and Earn) लिंक दिसते. इथे वाचकांना लॉगिन करुन मग इथले लेख, बातम्या वाचण्यास उद्युक्त केले जाते. यातून संस्थळाला त्यांचा वाचनाचा कल नि त्यावरील डेटा जमा करता येतो.

याशिवाय वेबसाईट लोड होताक्षणीच उजव्या बाजूला खाली एक व्हिडिओ दाखवणारी तरंगती (Floating) विंडो (मूळ पानाचा भाग नव्हे)दिसू लागते. एखादा लेख/बातमी बराच वेळ ओपन राहिली, तर खाली पण डावीकडे स्टार रेटिंगची (star rating) अशीच तरंगती विंडो ओपन होते. हिच्याद्वारे वाचकाने त्या लेख वा बातमीला आपल्या मतानुसार रेटिंग द्यावे अशी अपेक्षा असते. हे चारही कोपरे वापरुन झाले, आता मध्यभागाची पाळी येते. थोड्या वेळाने एक मोठी तरंगती विंडो मध्यभागी ओपन होते. यावर सहा लेखांची शिफारस केलेली असते.

इतके पुरे नसते म्हणून वरच्या बाजूला विविध मेन्यूही दिसतात; ज्यात गावांनुसार, विषयानुसार वर्गवारी निवडून केवळ त्यांच्याशी संबंधित लेख वाचण्याची सोय करुन दिलेली आहे.

आता एखादा लेख बातमी निवडून तुम्ही उघडता. लेख/बातमी यांच्या मजकुराच्या अधेमध्ये त्या लेखातील काही महत्वाचे शब्द वा विषय यांच्याशी संबंधित अन्य लेखांच्या लिंक्स ’क्लिक करा आणि वाचा’ या जाहिरातस्वरूपात दिलेल्या असतात. या खेरीज यू-ट्यूबप्रमाणे उजवीकडे एक समास ठेवून, त्यात ताज्या लेखांची सूचीही दिलेली असते. त्याशिवाय एक व्हिडिओंची सूची, आणि त्याखाली ’ट्रेडिंग टॉपिक्स’ची आणखी सूची असते. लेख/बातमीचा शेवट आला की खाली पुन्हा ’संबंधित स्टोरीज’चा स्लाईड-शो दिसतो, ज्यावरुन पुन्हा अन्य लेखांकडे जाता येते.

त्याच्या खाली ’महत्त्वाचा लेख’ म्हणून आणखी एका लेखाची शिफारस दिसते. वरचा स्लाईड शो इमेजेसचा आहे, तर हा फक्त शीर्षकांचा असतो. एवढे पुरेसे नसते; एक लेख संपला, की लगेच खाली पुढचा सुरू होतो. तुम्हाला क्लिकही न करता ’पुढचे पान’ वाचण्यास सुरुवात करता येते

महाराष्ट्र टाईम्सची ही वेबसाईट एखाद्या बँकेच्या, आयटी कंपनीतल्या अकाऊंट मॅनेजरच्या गळेपडूपणालाही लाज आणेल इतके फासे, इतकी जाळी वाचकाभोवती टाकून त्याला जखडून ठेवण्याचा प्रयत्न करत असते. या अनेक पर्यायांपैकी आपल्या लेखनाला पूरक ठरणारे, आणि आपल्या मते वाचकाला त्रासदायक वाटणार नाहीत, असे पर्याय निवडून आपल्या ब्लॉगवर समाविष्ट करत वाचकाला त्यावर अधिकाधिक काळ रेंगाळण्यास, वाचण्यास उद्युक्त करता येईल.

केल्याने प्रसिद्धी

तुमचे लेखन वृत्तपत्रांत वा नियतकालिकांमध्ये प्रकाशित केलेत तर प्रसिद्धीसाठी तुम्हाला वेगळे काही करावे लागत नाही. कारण ही माध्यमे जनमाध्यमे आहेत. त्यांचे ग्राहक आधीच निश्चित आहेत, ती त्यांच्यापर्यंत पोहोचतच आहेत. ब्लॉगचे तसे नाही. ते तुमचे खासगी माध्यम आहे. त्यामुळॆ त्याच्यावरील लेखनाच्या प्रसिद्धीसाठी तुम्हाला स्वत:ला खास प्रयत्न करावे लागतात.

शिफारस ही तुमच्या ब्लॉगच्या अखत्यारितला मामला होता. पण त्या बाहेरही तुमच्या लेखनाची जाहिरात करायची, तर पहिला पर्याय आहे तो ब्लॉग संग्राहक(aggregators). यांचा उल्लेख पहिल्या भागात आला आहे. हे ब्लॉगसाठी एखाद्या वृत्तपत्रांसारखे काम करतात. अनेक जण आपले ब्लॉगवर लेखन करतात/पोस्ट लिहितात, नि हे संग्राहक त्यांना एका जागी उपलब्ध करुन देतात. ज्याप्रमाणे सकाळी वृत्तपत्र वाचतो, त्याप्रमाणॆ हा संग्राहक उघडून एक एक लेखन वाचत जाता येते.

 ब्लॉग सुरु केल्यावर एकदाच तो इथे रेजिस्टर केला की काम झाले. पुढे जेव्हा जेव्हा तुम्ही नवीन पोस्ट लिहाल, तेव्हा त्या पोस्टचे शीर्षक आणि थोडासा मजकूर हे संग्राहक आपल्या सूचीमध्ये समाविष्ट करतात. तिथे भेट देणारे वाचक आपल्या रुचीनुसार वेगवेगळ्या ब्लॉगलेखकांच्या पोस्ट्स वाचू शकतात. मला स्वत:ला मराठी ब्लॉग लिस्ट (https://marathibloglist.blogspot.com/) मराठी ब्लॉग्स (https://marathiblogs.in/) आणि मराठी ब्लॉगर्स (https://www.marathibloggers.net/) हे तीन संग्राहक उपयुक्त ठरले आहेत.

पुढचा लोकप्रिय पर्याय आहे तो अर्थातच समाजमाध्यमांचा. व्हॉट्स-अ‍ॅप (WhatsApp), टेलेग्राम(Telegram) आणि फेसबुक यांसारख्या समाजमाध्यमांमध्ये ब्लॉगवरील लेखनाची लिंक शेअर करणे प्रसिद्धीसाठी उपयुक्त ठरते. इथेही बरेच संभाव्य वाचक एका संख्येने उपस्थित असल्याने लेखनाची त्यांच्यासमोर आयती जाहिरात करुन घेता येते. व्हॉट्स-अ‍ॅपवर फेसबुकच्या 'स्टोरी'प्रमाणेच ’स्टेटस्‌’ नावाचा प्रकार आहे. दोन्हींकडे हे प्रकार चोवीस तास दिसत राहतात, नि नंतर नाहीसे होतात. फेसबुक-पोस्ट आणि व्हॉट्स-अ‍ॅप वा टेलेग्रामवरील वैय्यक्तिक मेसेज हा मात्र स्थिर पर्याय आहे.

नुसती लिंक शेअर करण्याऐवजी, चित्रपटाचा ट्रेलर असतो त्या धर्तीवर थोडा मजकूर आणि लिंक शेअर केल्यास लिंकवर क्लिक करुन लेखन वाचले जाण्याची संभाव्यता बरीच वाढते. पण असे करण्यात एक धोका म्हणजे तेवढाच मजकूर ही पोस्ट समजून, संदर्भ ध्यानात न घेता तिचे आकलन केले जाऊ शकते नि प्रतिसाद दिला जाऊ शकतो. याखेरीज काही मंडळी फेसबुकवर शेअर करताना अनेक संभाव्य वाचकांना टॅग करण्याचा मार्ग वापरतात. मला स्वत:ला इतका गळेपडूपणा आवडत नाही. अगदी व्हॉट्स-अ‍ॅप वा टेलेग्रामवरही मोजक्या दहा लोकांना मी नव्या लेखनाची लिंक पाठवत असतो. यातही प्रामुख्याने फेसबुकवर नसलेल्यांचा समावेश असतो.

त्या पलिकडे काही जण म्हणतात की, ’पुरे लेखनच इथे - म्हणजे फेसबुक वा व्हॉट्स-अ‍ॅप वा टेलेग्राम चॅट विंडोमध्ये - पेस्ट करा, आम्हाला क्लिक करायचा कंटाळा येतो.’ आपल्या धोरणाचे समर्थन म्हणून ’फेसबुकवर लिंकपेक्षा कॉपी-पेस्ट केलेले लेखन अधिक पोचते’ असा दावा करतील. लेखक हा उत्पादक आहे आणि त्याने आपले उत्पादन आमच्या दारी येऊन विकतच नव्हे तर फुकट द्यावे हा माज मला अमान्य आहे.

माझे लेखन मी जर तुम्हाला फुकट वाचायला देतो आहे, तर निदान एक क्लिक करुन माझ्या ब्लॉगवर ते वाचावे, माझ्या ब्लॉगवरची वावरसंख्या एकने वाढवावी, हा माझा आग्रह अस्थानी आहे असे मला वाटत नाही. ’समोर आले तर वाचेन नाही तर आवर्जून येऊन वाचणार नाही’ असा त्यांचा बाणा असेल तर ’आझे लेखन वाचनीय असेल तर त्याचा वाचक माझ्या ब्लॉगवर येईलच’ हा माझाही बाणा आहे. त्यामुळे अशा ’द्या खाटल्यावरी’ वृत्तीच्या वाचकांकडे सरळ दुर्लक्ष करावे. हे लोक दोन शेपटांच्या उंदराचा व्हायरल झालेला व्हिडिओ आणि तुमचे लेखन, एकाच चवीने पाहात वा वाचत असतात. ’तुझे आहे तुजपाशी’मध्ये काकाजींनी ’जो वर्तमानपत्राचा कागद आणि केळ्याची साल एकाच चवीने खातो तो स्थितप्रज्ञ’ ही केवळ वैतागातून वा थट्टेने केलेली व्याख्या यांना तंतोतंत लागू पडत असते. 'हे आपले वाचक नाहीत' असे समजून सोडून द्यावे, निदान मी देतो.

ब्लॉगवरचे लेखन लिंक म्हणूनच फेसबुक वा व्हॉट्स-अ‍ॅपवर शेअर करण्याचा आणखी एक फायदा असा, की नक्की किती जणांनी हे लेखन उघडून पाहिले हे समजते. अलिकडचेच उदाहरण घ्यायचे तर ’कुराणाच्या संस्कृत अनुवादाच्या निमित्ताने’ हा लेख मी इथेच ’रमतारामाच्या विश्रांतीस्थळावर’ लिहिला नि फेसबुकवर शेअर केला. तिथे पंचाहत्तरहून अधिक लाईक्स होते आणि इकडे ब्लॉग जेमतेम पस्तीस वाचने दाखवत होता. फेसबुक लाईक्स किती फसव्या असतात याचे हे उत्तम उदाहरण.

कुणी म्हणेल, 'तुम्ही पुरा लेख तिथे टाकलात तर लाईकबरोबर वाचलाही जाईल.' पण हा दावा फुसका आहे. पोस्ट मोठी असली की फेसबुक पहिल्या काही ओळी दाखवून खाली 'See More'ची लिंक देतो. तुम्हाला आवश्यक वाटल्यास त्यावर क्लिक करुन पुरी पोस्ट उघडून वाचू शकता. ही जी मंडळी लाईक करतात, पण लिंकवर क्लिक करत नाहीत, ती ’See More’ या लिंकवरही क्लिक करत नाहीत असा माझा होरा आहे. (आणि 'त्यावर क्लिक करत असतील तर ब्लॉगलिंकवर का नाही?' हा माझा प्रश्न आहे.) त्यामुळे पुरा लेख तिथे पेस्ट केला, तरीही ते वाचणार नाहीत, फक्त लाईकचे देणे देऊन पुढे जाणार आहेत हे उघड आहे. त्यामुळे 'पुरा लेख तिथे टाकला तर अधिक वाचला जातो' यावर माझा विश्वास नाही. याउलट ब्लॉगवरील लेखन उघडणारा खरोखरच वाचण्याच्या उद्देशाने आलेला आहे हे गृहित धरता येते. उघडणार्‍यांपैकी बहुसंख्य वाचतही असतील असा माझा समज आहे.

तूर्त ब्लॉगबाबत इतके करून मी थांबलो आहे. या पलिकडे थीम्समध्ये काही प्रयोग करतो आहे. ते जमले तर याचा पुढचा भाग टाकेन. तोवर हॅपी ब्लॉगिंग.

- oOo -

पुरवणी : केल्याने प्रोग्रामिंग

या संपूर्ण लेखमालेमध्ये कोड आणि प्रोग्राम यांचा वारंवार उल्लेख आलेला आहे. Javascript, HTML, CSS या भाषांचाही. परंतु सार्‍या प्रवासाचे दस्त ऐवजीकरण हा मुख्य हेतू आहे. त्यापलिकडे एखाद्या ब्लॉगलेखकाला आपला ब्लॉग अधिक उपयुक्त, अधिक वावर असलेला कसा बनवता येईल याच्याबद्दल यातून काही मिळावे असा हेतू आहे. प्रोग्रामिंग शिकवणे हा अर्थातच नाही. पण तरीही काही जणांकडे ते कौशल्य असेल, तर त्यांच्या मदतीसाठी काही संस्थळे/वेबसाईट्सचे पत्ते देऊन ठेवतो.

https://www.w3schools.in/ : सर्वात महत्त्वाची साईट. इथे Javascript, HTML आणि CSS या तीनही भाषांसाठी मदत( Help) उपलब्ध आहे. शिवाय एक सोपा एडिटर (Editor) उपलब्ध आहे, ज्यामध्ये तुमचे कोड/प्रोग्राम तुम्ही तपासून पाहू शकतात. क्वचित इथे व्यवस्थित चालणारा कोड ब्लॉगमध्ये चालत नाही असे होऊ शकते. प्रोग्रामिंगबाबत थोडी प्राथमिक माहिती असणारे ही समस्या दूर करु शकतात.

आणखी काही उपयुक्त संस्थळे/वेबसाईट्स:

ब्लॉगर कम्युनिटी: https://support.google.com/blogger/community?hl=en

कम्युनिटीवरील आधीच्या चर्चा: https://support.google.com/blogger/threads?hl=en

ब्लॉगरसेन्ट्रल: https://www.bloggersentral.com/

https://www.mybloggertricks.com

https://helplogger.blogspot.com/

https://probloggerplugins.blogspot.com/

माझी ब्लॉगयात्रा - ७ : मोबाईल-विशेष

माझी ब्लॉगयात्रा - ६ : अनुक्रमणिका आणि सूची << मागील भाग

( मागील भागाच्या शेवटी या भागाचे जे नाव दिले होते ते ’काही अनुभव’ असे होते. माझ्या वैय्यक्तिक, व्यावसायिक आयुष्यात उत्पादक/सेवादाते-ग्राहक संबंधांबाबत मला जे अनुभव आले, त्यातून जे आकलन झाले त्यांच्या आधारे तो भाग लिहिण्याचे नियोजन होते. त्या आकलनाच्या आधारेच ब्लॉगलेखनाच्या शिफारस व प्रसिद्धीसाठी काही तंत्र वापरले आहे. परंतु तो भाग अपेक्षेहून खूप मोठा झाल्याने आणि एक स्वतंत्र लेख म्हणून विकसित झाल्याने या मालिकेतून गाळून टाकला आहे. तो जेव्हा प्रसिद्ध होईल तेव्हा त्याची लिंक इथे समाविष्ट करेन.)

मोबाईलवर लेखनसूची?

मागील भागाच्या शेवटी म्हटल्याप्रमाणे ’सूची देण्याचा जो श्रम केला, तो मोबाईल थीमवर वृथा गेला’ असल्याने आता मोबाईल थीमची ही मर्यादा कशी दूर करता येईल याचा विचार करु लागलो. मोबाईल थीम्स या स्वत:च एक सूची असतात. समास नाहीत की या सूचीच्या वरच्या बाजूस काही समाविष्ट करता येईल इतकी मोठी जागा नाही. जागा आहे ती फक्त एखादी पोस्ट ओपन केल्यावर तिच्या तळाशी. वाचक आधीच स्क्रोल (scroll) करुन तिथे पोहोचलेला असतो. त्यात पुन्हा सूची स्क्रोल करत बसण्याची त्याची/तिची मानसिकता उरत नाही. मांडणीच्या सुबकतेचा विचार केला तरीही ते बरोबर दिसत नाही. पुर्‍या सूचीचा नाद सोडून केवळ एका पोस्टचे सजेशनच पोस्टखाली दिले तर...?

कोणत्याही ब्लॉगवर सर्वात अलिकडच्या पाच (हा आकडा तुम्हाला बदलण्याची सोय आहे) पोस्ट एकाखाली एक दिसतात आणि सर्वात तळाशी ’older Post’ किंवा ’जरा जुनी पोस्ट’ असे एक बटण वा लिंक असते. मोबाईल थीमवर पोस्टस नव्हे, तर पाच पोस्टची सूची दिसते. पण तिथेही खाली हा पर्याय दिसतो. ते बटन दाबून जुन्या पोस्टकडे गेलात की त्यासोबतच ’नवीनतर पोस्ट्स’ किंवा ’Newer Posts' हा पर्यायही दिसतो. हे दोन पर्याय एक प्रकारे तुम्ही पुस्तकाचे पानच उलटून पुढच्या पानाकडे जात असल्याचा आभास निर्माण करतात.

परंतु यात दोन तोटे आहेत. ही बटणे एकाहुन अधिक पोस्टची सूची/पान उघडतात. त्यानंतरच तुम्ही कोणत्या पोस्ट पाहू वा वाचू शकता हे तुम्हाला समजू शकते. शीर्षकदेखील तेव्हाच दिसते. याशिवाय हा पर्याय पोस्ट्स फक्त कालानुक्रमेच दाखवत जातो. एखादा वाचक तुमचा ब्लॉग नियमित वाचत असेल, तर त्याच्या दृष्टीने हे पर्याय कुचकामी आहेत. त्याऐवजी तिथे जर रॅंडम क्रमाने एखादी पोस्ट तिथे सुचवली गेली, तर कदाचित बर्‍याच जुन्या, न वाचलेल्या, पण वाचून विसरलेल्या पोस्टही वाचकाला शिफारस म्हणून दाखवता येतील. तुमच्या ब्लॉगचा उशीरा शोध लागलेल्या वाचकाला हे उपयुक्त ठरेल नि तुमच्या जुन्या पोस्ट्सच्या ’टीआरपी’साठीही.

याच धर्तीवर आता प्रत्येक पोस्टखाली आणखी एका पोस्टचे रेकेमेंडेशन दिले की एकप्रकारे पोस्ट्सची साखळी तयार होईल नि वाचक एकामागोमाग एक पोस्ट्स वाचू शकेल. परंतु हे सोपे नव्हते. एकतर पोस्टच्या खालची जागा ही ब्लॉग-थीमच्या म्हणजे ब्लॉगर या ब्लॉगमंचाच्या अखत्यारीतील तर विजेट्स ही ब्लॉगमालकाला दिलेली स्वतंत्र ओसरी!. ब्लॉगमालकाने काय करायचे ते तिथे करावे, थीमला हात लावण्याची वेळ त्याच्यावर येऊ नये हा उद्देश. याचे कारण असे की थीमच्या कोड/प्रोग्राममध्ये बदल करायचा तर काळजीपूर्वक करणे गरजेचे असते. तिथे झालेली चूक संपूर्ण ब्लॉगला भोगावी लागते.

त्याचवेळी मी माझ्या दुसर्‍या ब्लॉगवर ’रॅंडम पोस्ट रेकेमेंडेशन’चे विजेट टाकले होते. तेच इथे वापरावे असा विचार केला. पण हा Code/program Javascript मध्ये होता. यापूर्वी म्हटल्याप्रमाणे ही भाषा मी टाळण्याचा माझा प्रयत्न होता, कारण अनेक ब्राउजर (browser) ती टाळतात. आणि सोपी असल्याने एखादा किमान माहितगार प्रोग्रामर तिच्यात सहज बदल करुन तुमची वाट लावू शकतो. एवढेच नव्हे विजेटसाठी लिहिलेल्या त्या प्रोग्राममध्ये वापरलेले लॉजिक हे तसेच्या तसे थीममध्ये नेता येणार नव्हते. त्यामुळे ते थीमच्या भाषेत रुपांतरित करुन, थोडे बदल करुन, डेस्कटॉप/लॅपटॉपची थीम आणि मोबाईलची थीम अशा दोन्हीकडे मूळ थीम/मांडणीमध्येच घुसवून दिले. आता दोनही थीम्सच्या तळाशी ’हे वाचले का?’ शीर्षक असलेली एक चौकट येते. त्यात एका रॅंडम पोस्टचे शीर्षक आणि त्या पोस्टमधील थोडा मजकूर दिसतो. ही झलक पाहून वाचकाला ती पोस्ट वाचावी की नाही याबाबत निर्णय घेता येऊ शकतो. आधीच्या अगदीच माहित नसता मागे जाण्यापेक्षा हे थोडे बरे म्हणावे असे.

पण पोस्ट-शिफारसीचा हा पर्याय तेव्हाच उपयोगाचा असेल, जेव्हा वाचक ब्लॉगच्या मुख्य पानावरुनच प्रवेश करेल. एखाद्याकडे विशिष्ट पोस्टची लिंक असेल, नि ती क्लिक करुन तो वाचक थेट त्या पोस्टवरच आला, तर हा पर्याय त्याला/तिला उपलब्ध असणार नाही. आणि असा थेट येणारा वाचक तेवढेच वाचून चालता होण्याची शक्यता अधिक असल्याने, त्याला ब्लॉगवर पकडून ठेवण्यासाठी(ही कल्पना माझ्या व्यावसायिक आयुष्यात भेटलेल्या ’अकाउंट मॅनेजर’ या संकल्पनेमधून सुचली.) प्रत्येक पोस्टच्या तळाशी ही पोस्ट शिफारस यायला हवी हे मला लक्षात आले. त्यामुळे आता ’हे वाचले का?’ची चौकट मी प्रत्येक पोस्टच्या खाली समाविष्ट केली. यासाठी हा पर्याय केवळ दोन्ही थीम/मांडणींमध्येच नव्हे, तर पोस्टच्या मूळ आराखड्यामध्येच (template) मध्येही घुसवून दिले.

आणि एकदा हा पर्याय स्वीकारला तर केवळ मोबाईलसाठीच का, डेस्कटॉप/लॅपटॉप मांडणीतही तो सहज घुसवता आला. एरवी त्या मांडणीमध्ये विविध प्रकारच्या अनुक्रमणिका होत्याच. त्यामुळे तिथे तो गरज म्हणून नव्हे तर उपलब्ध आहे म्हणून आणि ’जाहिरात’ म्हणून समाविष्ट केला. आता नकळत मी प्रसिद्धी/जाहिरातीच्या टप्प्यामध्ये प्रवेश केला होता. पुढे इतर अनेक वेबसाईटवर हा प्रकार वापरलेला 'मला दिसू लागला’. या तंत्राचा चांगलाच उपयोग होऊन ब्लॉगचा दरमहा वावर चांगला वाढला.

पण मला हे पुरेसे वाटत नाही. कारण यात वाचकाच्या आवडीचा वा प्राधान्याचा विचार नाही. ज्याअर्थी त्याने सध्याची पोस्ट वाचली आहे, त्याअर्थी त्याच्या विषयामध्ये त्याला रस असावा असा तर्क करता येतो. त्यामुळे खरेतर सर्वस्वी रॅंडम पोस्टची शिफारस करण्याऐवजी, त्या वाचलेल्या पोस्टच्या वर्गीकरणांपैकी किमान एक वर्गीकरण समान असलेली पोस्ट सुचवली, तर ती उघडली जाण्याची शक्यता आणखी वाढते.

यासाठी प्रत्येक पोस्टला चिकटवलेल्या टॅग्स अथवा लेबल्सचा उपयोग करुन घेता येतो. दोन पोस्ट्सना एखादे लेबल सामायिक असेल तर त्यांच्यात काही समान आहे असे गृहित धरता येते. याचा वापर करुन प्रत्येक पोस्टला ’संबंधित लेखन/पोस्टस’ सुचवणे शक्य आहे. या कल्पनेच्या आधारे प्रत्येक पोस्टच्या खाली तीन संबंधित पोस्ट्स वाचकाला सुचवण्याची सोय करुन ठेवली.

केल्याने शिफारस

आपल्या लेखनाची जाहिरात करायची तर सुरुवात आपल्याच ब्लॉग अथवा ब्लॉग्समधून करता येईल. ही वेबसाईट आपल्याच ताब्यात असल्याने, आपल्याला हवे तिथे अन्य लेखांची शिफारस अथवा जाहिरात करता येते. कोणत्याही वेबसाईट अथवा ब्लॉगवर जाहिरात ही दोन प्रकारे दाखवली जाते. पहिला प्रकार म्हणजे टेक्स्ट-इन (Text-In), म्हणजे मजकुरामधील दोन पाठोपाठच्या परिच्छेदांच्या मध्ये आणि दुसरा म्हणजे मूळ विंडोवर दुसरी तरंगती (pop-up) विंडो दाखवून त्यावर.

पहिला प्रकार बराच जिकीरीचा आहे. या पर्यायामध्ये उत्पन्नासाठी स्वीकारलेली त्रयस्थ जाहिरात दाखवायची तर प्रोग्राम गुंतागुंतीचा होतो. कारण अशा जाहिराती मजकुराचा भाग नसून जेव्हा वाचक ते पान उघडतो त्या क्षणी निवडल्या जाऊन तिथे दाखवल्या जातात. तेच पान पुन्हा उघडले तर तीच जाहिरात दिसेल याची शाश्वती देता येत नाही, किंबहुना दिसूच नये अशी इच्छा असते. परंतु आपण त्रयस्थ नव्हे तर आपल्याच अन्य पोस्टची जाहिरात दाखवणार असल्याने जाहिरातही आपल्याच कह्यात असते. वर म्हटले तसे पोस्टच्या नि ब्लॉगच्या खाली जी रॅंड्म पोस्ट रेकेमेंडेशन जाहिरास्त म्हणून दाखवतो आहे, तीच पोस्टच्या अधेमध्ये दाखवणेही सहज शक्य आहे. परंतु निदान माझा ब्लॉग व्यावसायिक नसल्याने, आणि एक वाचक म्हणून मजकुराच्या मध्येच येणारा असा प्रकार मला स्वत:ला आवडत नसल्याने, पोस्ट/लेखन पुरे झाल्यावरच ती जाहिरात दाखवण्याचा पर्याय निवडला आहे.

अनेक वृत्तपत्रांच्या वा तत्सम वेबसाईट्सवर लेख/बातमीच्या अधेमध्ये अन्य लेख/बातमीच्या लिंक्स अथवा व्हिडिओही घुसवून दिलेले दिसतात. अनेकदा त्या लिंक्स अनेकदा त्या मजकुराचा भाग नाहीत हे ही ध्यानात येत नाही. याचे कारण हीच मंडळी ’क्रॉस रेफरन्सिंग’(Cross-referencing) हा प्रकारही अनेकदा वापरताना दिसतात. म्हणजे एका बातमी अथवा लेखामध्ये अन्य बातमी वा लेखाचा उल्लेख आला (किंवा हेतुत: आणला), की तिथे उल्लेखालाच लेखाची/बातमीची लिंक चिकटवून दिलेली असते. या दोन प्रकारांची गल्लत होऊन वाचकाला वाचताना त्रास होतो. मी स्वत: हा शक्य तिथे हा क्रॉस रेफरन्सिंगचा पर्याय वापरतो. आणि म्हणून मजकुराच्या अधेमध्ये पोस्ट रेकेमेंडेशनची जाहिरात घुसवणे टाळतो.

हा मजकुराच्या गोंधळ टाळायचा असेल तर पॉप-अप (pop-up) विंडोचा वापर काही वेळा केला जातो. (पुढे maharashtratimes.com च्या केस स्टडीमध्ये याचा उल्लेख येईल.) परंतु हा ही प्रकार वाचकाला तापदायक असतो. एखादा लेख बातमी/वाचत असताना मध्येच एक विंडो येऊन ’या बातम्या वाचल्या का?’, ’महत्त्वाच्या बातम्या’ वगैरे शीर्षकाखाली दुसर्‍या कशाची शिफारस केली जाते. वैतागून ’अरे बाबा, जे वाचतोय ते तर पुरे होऊ दे.’ असे म्हणावेसे वाटते. अर्थात त्यांना याची थोडी जाणीव असल्याने एक लेख उघडल्यावर थोड्या वेळाने हा पॉप-अप येतो, बहुधा तो लेख वाचण्यास लागणार्‍या वेळाचा अंदाज घेऊन त्या नंतर.

पण असा अंदाज लढवण्यापेक्षा वाचक लेखाच्या/बातमीच्या तळाला पोहोचला, की मगच हा पॉप-अप देणे शक्य आहे. काही वेळा हा पर्याय वापरला जातो. परंतु यात किंचित धोका असा की वाचकाने वाचन मध्येच सोडून दिले, तर ही शिफारस येत नाही, आणि वाचक निसटून जाण्याची शक्यता वाढते. तरीही मध्येच येणारा पॉप-अप हा आता बहुतेकांचा नावडता प्रकार आहे. लॉगिन सक्तीचे असलेल्या वेबसाईट्स वगळता आता तो फारसे कुणी वापरत नाही.

त्याऐवजी ’स्लाईड-इन’(Slide-in) विंडोचा वापर होतो. लेख/बातमी जसजसा खाली स्क्रोल होत जातो तसतसे उजव्या बाजूच्या खालच्या कोपर्‍यातून (काही ठिकाणी उजव्या अथवा डाव्या बाजूला कडेला गेल्यावर) पॉप-अप सारखीच एक छोटी विंडो सरकत आत येते. यावर जाहिरात वा शिफारस दिली जाते. ही छोटी विंडो कोपर्‍यात असल्याने मूळ मजकुराला अडथळा करत नाही. तसंच पुन्हा उलट दिशेने स्क्रोल केले, तर ती गायबही होते.

पण या दुसर्‍या प्रकारात एक मोठा अडथळा आहे तो पॉप-अप ब्लॉकरचा. बहुतेक ब्राउजर आता पॉप-अप ब्लॉकर्स (pop-up blockers) सह येत असल्याने, हे पॉप-अप अथवा स्लाईड-इन पॉप-अप उघडलेच जात नाहीत. परंतु यावर आता बहुतेक प्रसिद्ध वेबसाईट्सनी उपाय शोधला आहे. या विंडोज पॉप-अप म्हणून न उघडता सरळ नवे पान म्हणून उघडतात, आणि आपल्या स्क्रिप्ट/कोड द्वारे त्यांचा आकार लहान करतात. अर्थात हे व्यावसायिक वेबसाईट्सना शक्य आहे. ब्लॉगमध्ये इतके गुंतागुंतीचे प्रोग्रामिंग करणे म्हणजे ’मियाँ बोटभर नि दाढी हातभर’ अशी अवस्था व्हायची. तरीही काही स्लाईड-इन विजेट्स उपलब्ध आहेत. परंतु ती अपेक्षेप्रमाणे काम करत नसल्याने मी वापरलेली नाहीत.

तुमचे एकाहुन अधिक ब्लॉग असतील, तर एका ब्लॉगवरील लेखनाची सूची अथवा शिफारस दुसर्‍या ब्लॉगवर देऊन एका ब्लॉगच्या वाचकाला दुसर्‍या ब्लॉगवर खेचून नेता येते. यात वर दिलेले पोस्ट शिफारसींचे सर्व पर्याय वापरता येऊ शकतात. त्या पलीकडे मी वापरलेला पर्याय म्हणजे मार्की (Marquee) अथवा सरकती पट्टी. मी हा पर्याय निवडला याचे कारण पुन्हा मोबाईल थीमची मर्यादा. अशा जास्तीच्या माहितीसाठी मला तिथे फक्त पोस्टसूचीच्या वर जागा मिळते. तिथे मला उभी सूची देणे शक्य नसते, कारण याच ब्लॉगमधील लेखांची सूची खाली सरकून कदाचित स्क्रीनबाहेर जाईल. म्हणून मी उभ्याऐवजी आडव्या सूचीचा विचार केला.

पण मोबाईल स्क्रीनची रूंदी फारच कमी असल्याने, ती सूची स्थिर असली तर जेमतेम एकाच लेखाचे शीर्षक तिथे दिसू शकेल. त्याऐवजी तिला सरकती ठेवली तर अन्य ब्लॉगवरील अलीकडच्या काही पोस्टच्या लिंक्स मी तिथे देऊ शकतो. हा प्रकार द्यायला तसा सोपा कारण तो HTML भाषेत ही तयार मिळते. पण यात फार काही बदल करता येत नाही्त. शिवाय हे आता 'बाहेरच्या वाटेवर' (deprecated) असल्याचे जाहीर केले असल्याचे समजल्यामुळे, ते बदलून CSS कोड वापरून ही मार्की अथवा सरकती पट्टी तयार केली. माझ्या दोनही ब्लॉग्सवर एकमेकांच्या अलिकडच्या लेखांची सूची या सरकत्या पट्टीद्वारे मी देऊन ठेवली आहे.

(क्रमश:)

    पुढील भाग >> माझी ब्लॉगयात्रा - ८ : केल्याने प्रसिद्धी

कुराणाच्या संस्कृत अनुवादाच्या निमित्ताने

बातमी: कुराणाचा प्रथमच संस्कृतमध्ये भावानुवाद ; दिवंगत पंडित गुलाम दस्तगीर बिराजदार यांच्या ग्रंथाचे शुक्रवारी प्रकाशन
---

काही काळापूर्वी जावेद अख्तर यांचे रेख़्ता या वार्षिक उर्दू संमेलनातील भाषण ऐकले होते, त्यावर ’वेचित चाललो...’ वर (’भाषा: राष्ट्र, धर्म... आणि हत्यार’) लिहिलेही होते.

त्या भाषणादरम्यान त्यांनी केलेला एक उल्लेख मला रोचक वाटला होता. ते असं सांगतात की, १७९८ मध्ये कुराण प्रथम उर्दूमध्ये अनुवादित केले गेले. त्यावेळी ’असल्या अमंगळ भाषेत आमचे पवित्र पुस्तक लिहिले’ म्हणून तो अनुवाद करणार्‍याविरोधात मौलवींनी फतवा काढला होता. त्याचवेळी ’असल्या अमंगळ भाषेला ’देव’नागरी नावाने ओळखळी जाणारी आमची पवित्र लिपी वापरल्याने ती विटाळेल’ असा विरोध हिंदू समाजातील संभावितांनी केला होता. ’अमंगळतेच्या कल्पना अमंगळ मनातूनच येतात’ हे माझे मत काहीसे दृढ करणारी ही दोन उदाहरणे. दोनही धर्मांतील सनातन्यांच्या नाकावर टिच्चून ऊर्दू वाढली नि लोकप्रिय झाली. त्यातील सुरुवातीचे साहित्यही प्राधान्याने विद्रोही होते, धार्मिक नव्हते हे उल्लेखनीय.

पण जुन्या चुकांतून माणसे शिकत नाहीत. तसे होते, म्हणून इतिहास शिकावा म्हणणारे लोक धूर्त असतात. इतिहासातून ते आपले झेंडे नि जोडे, हीरो नि सैतान निवडत असतात आणि त्या आपल्या धारणा बहुसंख्येच्या बोकांडी मारण्यासाठीच त्यांना तो रुजवायचा असतो. या समाजात स्वत:हून शिकण्याला परंपरा नाही. तो विद्रोहाचाच भाग असतो. आणि इतिहासातून कुणी विद्रोह शिकतो असे मला वाटत नाही. किंबहुना विद्रोह हा आतून उमटतो, इतरांच्या विद्रोहाची नक्कल म्हणजे विद्रोहच नव्हे. असला विद्रोहदेखील एक परंपराच बनून राहतो. ’ब्लॅक मिरर’ विज्ञान-काल्पनिकेमधील ’फिफ्टिन मिलियन मेरिट्स’ या एपिसोडमध्ये उपभोगवादाच्या विरोधातील कुण्या बिंगचा विद्रोह क्रयवस्तू बनून विकला जाऊ लागतो तसे.

त्यामुळेच तेव्हाचा उर्दूचा इतिहास शिकूनही आज फारशी समज वाढलेली नाही. संस्कृत ही ब्राह्मणांची आणि उर्दू ही मुसलमानांची म्हणून तिचा तिरस्कार करणे याला विद्रोह वगैरे समजले जाऊ लागले आहे. अख्तरांच्या भाषणाच्या निमित्ताने लिहिलेल्या लेखामध्ये भाषेचा ’हत्यार’ म्हणून कसा वापर झाला हे उर्दूच्या संदर्भात लिहिले होते. संस्कृतचाही तसाच वापर झालेला आहे असे म्हणता येईल.

पण या दोन्हींमध्ये त्या-त्या भाषेचा दोष अर्थातच नाही. कारण भाषा मानवनिर्मित आहे, तिला स्वत:च्या अशा भाव-भावना नसतात. ती कुणाचा द्वेष करत नाही की कुणाला धार्जिणी असत नाही. भाषा घडते ती संवादाचे माध्यम म्हणून, घडवली जाते ती अनेक माणसांकडून. एक माणूस लिहायला बसला नि एक भाषा तयार केली असे होत नाही. किंबहुना भाषा हे संवादमाध्यमाला दिलेले औपचारिक रूपच असते. ज्यात लिखित वा मौखिक साहित्य निर्माण केले जाते ती अधिक रुजते. एखाद्या समाजाचा द्वेष करताना त्या भाषेचा द्वेष करणे, त्या भाषेला केवळ त्या समाजाच्या संदर्भातच पाहणे हा करंटेपणा आहे. आपल्याला ती भाषा शिकण्याची वा समजून घेण्याची इच्छा नसेल तर तसे न करणे हा आपल्या स्वातंत्र्याचा भाग आहे. जगात अक्षरश: हजारो भाषा आहेत, सार्‍यांतच आपल्याला रूची असणे शक्य नसते. म्हणूनच हिंदीची सक्ती हा निषेधार्ह आहे, तशीच संस्कृत वा ऊर्दूचीही.

माझे मत विचाराल, तर संस्कृत ब्राह्मणांची म्हणून तिचा तिरस्कार करण्याऐवजी त्या भाषेत भरपूर विद्रोही साहित्य निर्माण करुन एका बाजूला झुकलेल्या तराजूचे दुसरे पारडे जड करत न्यावे असे मला वाटते. शोषकांची भाषा म्हणून तिला अडगळीत टाकण्याचा आटापिटा करणे मला मान्य नाही. त्याच भाषेत धार्मिक वाङ्मयाबरोबरच नाट्यशास्त्रापासून आयुर्वेदाच्या अनेक अनुषंगापर्यंत, भास्कराचार्यांच्या लीलावती पासून कणादाच्या खगोलशास्त्रापर्यंत इतरही बरेच उत्तम लेखन झाले आहे. शोषक-समर्थक लेखनासाठी अख्खी भाषा बुडवावी हे म्हणणे विचारहीनतेचे लक्षण आहे... तिथे कम्युनिस्ट आहेत म्हणून जेएनयूसारख्या एका सर्वोत्कृष्ट विद्यापीठाला शक्य त्या सार्‍या माध्यमांतून बदनाम करण्याचा आटापिटा करण्याइतकेच !

हीच बाब उर्दूबाबत अख्तरांनी नोंदलेली आहे. ते पंजाबी तरुणांना विचारतात, ’अरे ही तुमची भाषा आहे. यातले सर्वात दर्जेदार साहित्य तुम्ही- पंजाबींनी- निर्माण केले आहे. आता अमुक धर्माची भाषा म्हणून तुम्ही तिला दुसर्‍यांच्या ओटीत कसे घालता. तुम्ही ती स्वीकारली पाहिजे त्यात तुमच्या मातीतले साहित्य निर्माण केले पाहिजे.’

www.naidunia.com येथून साभार.

आज कुराणाचा संस्कृतमध्ये केलेला अनुवाद प्रसिद्ध होतो आहे, एक भिंत तुटते आहे. दुर्दैवाने त्या बातमीतही ’जन्माने मुस्लिम असले तरी...’ असा दुर्भाग्यपूर्ण उल्लेख वाचावा लागतो आहे. संस्कृतचे कितीही गाढे पंडित असले तरी ’मुस्लिम असूनही’ हा hyphenated(याला नेमका मराठी प्रतिशब्द सापडला नाही) विचार बातमीदारालाही टाळता आलेला नाही. केवळ ’कुराणाचे संस्कृत भाषांतर/अनुवाद’ इतकाच विचार करुन त्याला थांबता आलेले नाही.फोटोही गळ्यात ’भगवे’ उपरणे असलेला निवडला आहे! आजच्या द्वेषसंपृक्त काळात त्याच्याकडे अशा दूषित दृष्टीनेच पाहिले जाणार आहे. बिराजदार हे मूळचे सोलापूरचे (बहुधा तेव्हाच्या मराठवाडा विद्यापीठातही त्यांनी शिकवले, मला हे नक्की आठवत नाही आता.) त्यामुळे उलट दिशेने ’तुम्ही पुण्या-मुंबईचे लोक...’ हा प्रांतवादही खेचून आणता येईल. ’आम्ही हिंदू आहोत, आम्ही यास्मिन शेख यांचे व्याकरण अभ्यासत नाही. आमच्याकडे फडकेंचेच पुस्तक असेल.’ असे आयुष्यात व्याकरणाचा ’व्य’देखील न व्यायलेल्या निर्बुद्धांकडून ऐकण्याचे दिवस आहे्त. यात काही कारण नसताना यास्मिन शेख विरुद्ध फडके ही कदाचित दोघांच्या गावीही नसलेली विभागणी गलिच्छ मंडळी करत आहेत, त्यांना सत्तेचा आशीर्वाद आहे आणि कणाहीन बहुसंख्येचा मूक वा नाईलाजाने उघड पाठिंबा.

आपापल्या धर्मातले साहित्य, धर्मग्रंथ हे अन्य भाषेत नेणे याला केवळ धर्मप्रसाराचाच भाग समजणारी मंदबुद्धी बहुसंख्या बरीच असते. मुळात सतत गमावण्याची भीती असणार्‍या या जनतेला यातून परस्पर सांस्कृतिक ओळख, अभ्यास नि आदानप्रदान होऊ शकते याची जाणीव नाही. ज्यांना आहे त्यांना नेमकी त्याचीच भीती आहे. सतत प्रत्येक गोष्ट पावित्र्याच्या प्रेतवस्त्रात गुंडाळून पूजणार्‍यांना बदल नको असतात. आणि म्हणूनच ’आमच्याकडे पुराणां-कुराणांतून वा दास कॅपिटलमधून आलेले संपूर्ण ज्ञान आहे. आम्हाला इतरांकडून काही शिकण्याचे शिल्लकच नाही’ असा यांचा दावा असतो. त्यामुळे असे प्रयत्न आजच्या ’द्वेष करा, कळपात राहा’ समाजातच नव्हे, तर एरवीही कायम दुर्लक्षित राहतात.

माझी खात्री आहे एरवी गीतेबरोबरच कुराणाचा अभ्यासही सारखाच मानणार्‍या इतर समाजापेक्षा तुलनेने समतोल असणार्‍या पुरोगामी वर्तुळातही याचे स्वागत थंडपणे केले जाणार आहे. कुराण धार्मिक म्हणून तटस्थ राहावे, एका मुस्लिम विद्वानाने संस्कृतचा केलेला व्यासंग म्हणून नावाजावे की संस्कृतचे अप्रत्यक्ष कौतुक होईल नि पुरोगामी वर्तुळाचा एक भाग आपल्याला शोषितांचे समर्थक म्हणून वाळीत टाकतील या संभ्रमात ते मुकाट राहणेच पसंत करतील. एका तटस्थ मित्राने ’विज्ञानवादी सावरकर’ या विषयावर चर्चा आयोजित केली असता, अशाच भीतीने बहुतेक पुरोगामी मंडळींनी त्यापासून दूर राहणे पसंत केले होते. वास्तविक ’सावरकरांचा विज्ञानवाद हा त्यांच्या हिंदुत्ववादाचे अपत्य आहे’ हे त्यांचे एरवी मांडले जाणारे मत तिथे विस्ताराने मांडण्याची संधी होती. पण सावरकर या नावामुळेच आपण ’घराबाहेर’ काढले जाऊ ही भीती त्यांच्या मनात होती. हिजाबबाबत गदारोळाच्या वेळेसही अनेकांच्या मनात असा तिढा उत्पन्न झाला होता. मी हे लिहितो म्हणून दुसर्‍या बाजून खुश व्हायचे कारण नाही. त्यांच्या मनात संभ्रम आहे कारण ते विचार करतात. तुमच्या मनात संभ्रम नसतो कारण तुम्ही एक बाजू आंधळेपणे उचलायची हे ठरवल्याने विचार नि तुमचा संबंध येत नसतो, त्यामुळे संभ्रमाचा प्रश्नच येत नाही.

मला स्वत:ला शाळेतील अभ्यासाखेरीज टिळक महाराष्ट्र विद्यापीठाच्या तीन परीक्षा देऊनही संस्कृत कधी आपली वाटली नाही. कळत्या वयाच्या सुरुवातीच्या ज्या काळात हिंदुत्ववाद्यांच्या प्रभावाखाली होतो, तेव्हाही ’आपण हिंदू, त्यातही ब्राह्मण घरात जन्माला आलो म्हणजे तिचा अभिमान बाळगला पाहिजे’ असे वाटले नाही. त्याचबरोबर, ’मला आवडली नाही वा माझे तिचे नाते जुळले नाही, म्हणजे ती भाषाच वाईट वा दुय्यम आहे’ असा कांगावा करुन वा सिद्ध करण्याचा आटापिटा करुन तो इतरांच्या गळी उतरवावा असेही मला कधी वाटलेले नाही. त्याच काळात- अद्याप हिंदुत्ववाद्यांच्या प्रभावात असताना- संस्कृतपेक्षा उर्दू अधिक भावली. त्यातील शायरीमधून झालेली विचारस्वातंत्र्याची ओळख जशी महत्वाची वाटली, तसेच त्यातील कानावर पडलेल्या एक न एक गजलेचा अर्थ उर्दू-मराठी शब्दकोष वाचून समजून घ्यायलाच हवा इतके तिच्याशी घट्ट नाते जुळले. कदाचित तोवर डोक्यातील विचारांचे इंद्रिय जागे झाल्याने तिचे विद्रोही असणे आवडले असेल.

पण अशी आवडनिवड सापेक्ष असते, एका डेटा पॉईंटवर संपूर्ण भाषेबाबत निवाडा करावा हे तेव्हा संख्याशास्त्र शिकणे सुरु झालेले नसूनही समजत होते. तसंच बहुसंख्येने याचा निवाडा करणेही हास्यास्पद असते. कारण तसे असेल तर गणित हा बहुसंख्येने बाद विषय ठरेल. आणि ते नष्ट होताना तयार झालेल्या ब्लॅक-होलमध्ये सारे विज्ञान आणि म्हणून सारी मानवी प्रगती नाहीशी होऊन जाईल. मानवाची प्रगती ही नि:संशय विज्ञानाची प्रगती आहे धर्मग्रंथांची नाही! त्यामुळे केवळ आपल्याला रुचते, जमते ते स्वीकारले, जे नाही ते सोडून दिले इतके सोपे असते. यामुळे ’माझेच बरोबर’ या न्यायाने ही भाषा ग्रेट नि ती दुय्यम असा निवाडा मी दिलेला नाही.

भाषांना राष्ट्रवादाचे वा जातीयवादाचे हत्यार समजणे हा मानवी मनाचा मोठा आजार आहे आणि तो फारच सार्वत्रिक आहे. आणि अस्मितेसह इतर अनेक आजारांसह आपण सोडून सगळ्यांना तो आहे असा आपला भ्रम असतो. प्राणिसृष्टीचा भाग म्हणून विचार केला तर बांधिलकीपेक्षा वाळीत टाकणे अधिक आवडणारा माणूस हा एका बाजूने कळपप्रधान शेळ्यांसारखा असतो आणि त्याचवेळी आपण सिंहासारखे आहोत, इतर नरांना माझ्या कळपात जागा नाही हे त्या कळपात सुरक्षित राहूनच तो गर्जून सांगत असतो. त्यामुळे त्याचे तथाकथित शौर्य हे केवळ कळपाबाहेरच्यांबाबतचा द्वेष या स्वरूपातच शिल्लक राहते. आणि ते ही शिल्लक राहावे म्हणून कळपाबाहेरचे लोकही शिल्लक राहावे लागतात... मग ते राजकारण असो, समाजकारण असो की भाषाकारण.

हे सारे विचार ज्यांच्या निमित्ताने उमटले त्या दिवंगत पं. गुलाम दस्तगीर बिराजदार, त्यांनी आयुष्यभर जपलेले संस्कृतप्रेम यांना एक मानाचा मुजरा करता आला तरी खूप झाले.

- oOo -

माझी ब्लॉगयात्रा - ६ : अनुक्रमणिका आणि सूची

माझी ब्लॉगयात्रा - ५ : मजकूर सुरक्षितता << मागील भाग
---

ब्लॉगच्या मजकुराची शक्य तेवढ्या सुरक्षिततेची सोय केल्यावर आता पुढच्या टप्प्यात विचार करायचा, तो ब्लॉगच्या सुशोभीकरणाचा. त्यासाठी कोण-कोणत्या गोष्टी, बाबी वा पर्याय वाचकाला उपयुक्त ठरु शकतात याचा विचार करायला हवा. हा विचार तुमच्या ब्लॉगमधील विषयांच्या अनुषंगाने व्हावा. एका प्रकारच्या ब्लॉगसाठी जे तंत्र कामात येईल, तेच सर्व प्रकारच्या ब्लॉग्सना लागू असेल असे नव्हे. व्यावसायिक ब्लॉग्समध्ये उपयुक्त ठरणारे पर्याय साहित्यिक लेखनाच्या ब्लॉगमध्ये तितकेच उपयुक्त असतील असे नाही. आणि तिथे उपयुक्त असणारे पर्याय हे प्रासंगिक लेखनाच्या, 'सुचले तसे' अथवा run of the mill प्रकारच्या लेखनाच्या ब्लॉगवर कामात येतील असे नाही.

बहुतेक ब्लॉगमंचांवर तुमच्या पोस्ट्सची अनुक्रमणिका तयार करणारे विजेट (widget) असते. डाव्या वा उजव्या समासात ते समाविष्ट केले, की त्या अनुक्रमणिकेतून हव्या पोस्टच्या शीर्षकावर क्लिक करुन ती पोस्ट उघडता नि वाचता येते. ही अनुक्रमणिका अर्थातच कालानुक्रमे केलेली सूची असते. तुमच्या ब्लॉगवरील सर्व पोस्ट्सची सूची देणारे ’ब्लॉग-सूची’ (Blog-Archive) नावाचे तयार विजेट ब्लॉगरमध्ये येते. त्यात सर्वात प्रथम वर्ष, प्रत्येक वर्षांच्या आत महिने आणि प्रत्येक महिन्यांच्या आत - हवे असल्यास - आठवडे आणि अखेरीस दिनांक असा Tree किंवा उतरती भाजणी असते. हव्या त्या वर्षावर क्लिक करुन त्या महिन्याची वा आठवड्याची पोस्ट-सूची उघडून पाहता येते.

परंतु यात एक समस्या आहे. समजा मी पूर्वी तुमच्या ब्लॉगवर एक लेख वाचला होता. त्याचे नावही मला आठवते, परंतु तो प्रकाशित झाल्याचा दिनांक अर्थातच आठवत नसतो. त्यामुळे मला ब्लॉग-सूचीमधून तो लेख शोधणे अवघड जाते. अशा वेळी तुमच्या ब्लॉगवर कालानुक्रमे पोस्ट-सूची जशी असते तशीच अकारविल्हेही (alphabetical) दिलेली असेल तर तो लेख शोधणे मला सोपे जाते.

कुणी म्हणेल शीर्षक ठाऊक असेल तर सर्च पर्याय वापरता येईल. ते बरोबरच आहे. परंतु हा पर्याय अपेक्षित निकाल देतोच असे नाही. विशेषत: देवनागरी लिपीतील मजकुराचा शोध अनेकदा अपेक्षित त्या मजकुरापर्यंत पोहोचवत नाही. शिवाय मला लेखाचे जे नाव आठवते आहे त्यात माझ्या स्मरणशक्तीमध्ये गफलत असेल, तर मला हवी ती पोस्ट सापडणारही नाही. आणखी एक सुप्त हेतू जाहिरातबाजीचाही आहे. सूची स्क्रोल करत असताना त्यातील इतर लेखांची शीर्षके पाहून ’हा ही वाचून पाहू’ अशी उत्सुकता वाचकाच्या मनात नकळत निर्माण होऊ शकते. त्यातून त्याचा/तिचा तुमच्या ब्लॉगवरचा वावर वाढू शकतो. या ब्लॉगवर डावीकडच्या समासात कालानुक्रमे नि अकारविल्हे अशा दोनही सूची दिलेल्या आहेत. यातील अकारविल्हे सूची तयार करण्याचा कोड मला तयारच मिळाला नि मी तो समाविष्ट केला.

याखेरीज काही वेळा दीर्घ लेखन हे एकाहुन अधिक भागात, एका मालिकेच्या स्वरूपात लिहिले जाते. किंवा वेगवेगळे लेख एका सूत्राने बांधले जाऊन (उदा. यावर्षीच्या ऑस्कर नॉमिनेटेड चित्रपटांबद्दलचे लेख) एक मालिका तयार होत असेल तर असे लेख वाचकाला एका पाठोपाठ एक वाचता यावेत यासाठी या मालिकांची स्वतंत्र सूची देणे उपयुक्त ठरते. ब्लॉगसूचीच्या धाटणीची उघड-बंद पद्धतीची सूची मी अशा मालिकांसाठी समाविष्ट केली आहे. एकाच मालिकेतील लेख शोधाशोध करत न बसता, एकाच सूचीतून उघडणे शक्य होते. दुर्दैवाने नवी पोस्ट उघडताना ब्लॉगर समासातील विजेटसह सर्वच नव्याने उघडत असल्याने विजेटची मागची स्थिती राखली जात नाही. पुढच्या लेखासाठी मला ते विजेट पुन्हा उघडून सूचीमध्ये जावे लागते.

याशिवाय तुमच्या ब्लॉग-लेखनाचे विविध categories मध्ये वर्गीकरण करता येते. यासाठी प्रत्येक पोस्टला काही लेबल्स/टॅग्स/कॅटेगरीज चिकटवण्याची सोय असते. उदाहरण द्यायचे तर एखाद्या खादाडीच्या (Foodie) ब्लॉगवर हैदराबादमधील एखाद्या प्रसिद्ध बिर्याणी सेंटर/होटेलच्या मुशाफिरीबद्दल लिहिताना त्यावरील पोस्टला गावाचे नाव म्हणून हैदराबाद, होटेलचे नाव आणि बिर्याणी अशी तीन लेबल्स चिकटवता येतील. पोस्टच्या खाली दिसणार्‍या या लेबल्सपैकी एकावर क्लिक केले असता ते लेबल मिरवणार्‍या सर्व पोस्ट्स एकाखाली एक दिसू लागतात. एखाद्या वाचकाला त्या ब्लॉगवरील फक्त बिर्याणीबद्दलच्या पोस्ट वाचायच्या असतील तर ती पोस्ट त्या गटात दिसेल, किंवा हैदराबादला जाणार्‍याला तिथे कोणते पदार्थ नि कुठे खावेत असा प्रश्न असेल, तर त्या ’स्थान’ निश्चित करणार्‍या ’हैदराबाद’ या गटातही ती पोस्ट दिसेल.

पण पंचाईत अशी, की एका लेबलच्या बर्‍याच पोस्ट्स असतील तर भरपूर स्क्रोल करत जावे लागते. त्याऐवजी त्यांची यादी/सूचीच तयार करुन वाचकासमोर ठेवता आली, तर शीर्षकांकडे पाहून पोस्टची निवड करण्यास तुलनेने कमी वेळ लागेल. दुर्दैवाने निदान ब्लॉगरमध्ये अशी निव्वळ सूची तयार करणारे विजेट नाही. त्यासाठी स्वतंत्रपणे प्रोग्राम लिहावा लागतो. तिथे तुम्हाला category-cloud अर्थात वर्गवारी-पुंजका मिळतो. ज्यात सर्व लेबल्स/कॅटेगरीज एका पुंजक्याच्या स्वरूपात मिळतात आणि प्रत्येक लेबल असलेल्या पोस्ट्सच्या संख्येनुसार त्या लेबलच्या नावाचा आकार कमी-जास्त दिसत असतो. पण यातून कोणत्या वर्गवारीसाठी तुम्ही अधिक लेखन केले आहे हे दिसते इतएक्च. याच विजेटला लेबल-सूची स्वरूपातही समाविष्ट करता येते.

पण पुन्हा नवी समस्या अशी आहे, की एकुण ब्लॉगमध्ये भरपूर पोस्टस आणि म्हणून भरपूर लेबल्स/टॅग्सची जंत्री असते. प्रत्येकाची सूची देत बसलो तर त्या सूचींची एक सूची करावी लागेल. अर्थात वर उल्लेख केलेल्या ब्लॉग-सूची विजेटच्या धर्तीवर सर्व लेबल्स/टॅग्सची एक सूची देऊन नंतर प्रत्येक लेबलसाठी उपसूची दाखवता आली तर वाचकाला ते सोयीचे ठरेल. मी मूळ ब्लॉग-सूची विजेटचा प्रोग्राम/कोड घेऊन हा बदल करण्याचा प्रयत्न केला. पण तो भलताच गुंतागुंतीचा होऊ लागला म्हणून सोडून दिला.

आणखी मुद्दा असा की प्रत्येक लेबल/टॅग अथवा वर्गीकरण सारखेच महत्वाचे असेल असे नाही. त्यामुळे सर्वच टॅग्सची उपसूची तयार करण्याची बरेचदा गरजच नसते. मग केवळ महत्वाच्या अशा मोजक्या लेबल्ससाठीच ही सूची तयार करण्याचा निर्णय मी घेतला. ’वेचित चाललो...’ ब्लॉगसाठी विचार करताना मला सुमारे बारा लेबल्स अशी सापडली, की त्यांची स्वतंत्र सूची उपयुक्त ठरेल असे मला वाटले. आता या बरा सूची एकाखाली एक दिल्या, तर वाचकाला समासात बरेच स्क्रोल करत जावे लागेल असे लक्षात आले. एवढी सहनशक्ती व्हॉट्स-अ‍ॅप जेनेरेशनकडे असण्याची शक्यता फारच कमी आहे.

’वेचित चाललो...’ वर सुरुवातीला पुस्तकांचे वेचे नि त्याबद्दलचे लेखनच समाविष्ट केले होते. एकदा एका पुस्तकाचा वेचा तिथे समाविष्ट करुन झाल्यावर प्रूफरीडिंग करत होतो. हातातल्या पुस्तकाचे पान उलटताना आर्किमीडिजसारखाच माझाही ’युरेका’ क्षण सापडला. म्हटलं त्या बारापैकी प्रत्येक सूची हे एक पान धरले, तर पुढच्या लेबल-सूचीसाठी ’पान उलटावे’ लागेल. आणि हे टॅब्ड (tabbed) सूचीने साध्य करता येईल. ब्लॉगवर वरच्या बाजूला मेन्यूसारखी पेजेस (Pages) देण्याची सोय ब्लॉगरने केलेली आहे. त्यावर प्रत्येक सूचीसाठी एक पेज तयार करणे शक्य होते. परंतु पेजेसचा जीव मर्यादित असतो. एक पानाचा मजकूर या पलिकडे त्यावर फार काही करता येत नाही. म्हणजे त्यावरील बहुतेक गोष्टी या प्रोग्राम लिहूनच तयार कराव्या लागल्या असत्या. शिवाय निव्वळ सूचीसाठी संपूर्ण स्क्रीनचा वापर करण्याची गरजही नव्हती.

परंतु विजेटमध्ये टॅब तयार करण्याचे प्रयोग काही जणांनी केले होते. त्यातले काही निवडून माझ्या काही प्रयोगांनंतर त्यातील एक निवडला. परंतु या ना त्या कारणाने तो आहे असा वापरत येईना. पुन्हा प्रथम Javascript मधला कोड वापरला होता. तो पुरेसा 'वर्धनीय व तन्य’ (शाळेतले शब्द बर्‍याच दिवसांनी आठवले) नाही असे लक्षात आले. त्यातच अनेक ब्राउजर हे सुरक्षिततेच्या कारणास्तव Javascriptला बाहेरचा रस्ता दाखवण्याच्या मार्गावर आहेत हे समजल्यावर त्याला पर्याय शोधणे सुरु केले. मग HTML+CSS असा एक कोड मिळाला.

पण त्याचे स्वत:चे असे प्रॉब्लेम होते. त्यात पुन्हा त्यातील कोड हा देवनागरी लिपीतील शीर्षकांचा वापर केला तर गंमत करु लागला. याचे कारण म्हणजे तो कॅरॅक्टर (character) संख्येच्या गणितावर काम करत होता. पण देवनागरीमध्ये एक अक्षर हे एकाहुन अधिक कॅरॅक्टर्स वापरून लिहिले जाते. उदाहरणार्थ ’किती हा शब्द ’क+पहिल्या वेलांटीचे कॅरॅक्टर+त+दीर्घ वेलांटीचे कॅरॅक्टर’ असा चार जागांमध्ये लिहिला जातो. यातून रोमन लिपीसाठी लिहिलेला मूळ कोड जर देवनागरीसाठी वापरला तर अपेक्षित उत्तर मिळत नाही. त्यामुळे त्यात आवश्यक ते बदल करुन घ्यावे लागले.

त्यापुढे त्यासाठी आवश्यक त्या आकाराची चौकट तयार करणे, सूची तयार करण्याचा प्रोग्राम, सूचीचे स्वरूप, वगैरेसाठी काही प्रयोग करुन अखेर हवे तसे विजेट तयार झाले. माझ्या ब्लॉगच्या समासांच्या आणि निवडलेल्या लेबल्स/टॅग हे शीर्षक म्हणून येताना वापरल्या जाणार्‍या रुंदीचा विचार करुन एका विजेटमध्ये चार लेबल्सची सूची बसवणे निश्चित केले. बारा लेबल्ससाठी तीन वेगळ्या सूचींची योजना केली. हे तीन गट शक्यतो परस्परसंबंधित निवडले. व्हिडिओ या वर्गवारीशी निगडित चित्रपट, मालिका, चलच्चित्र (Animation) आणि लघुपट (short-film) अथवा एकुणच मर्यादित लांबीचा कुठलाही व्हिडिओ- या चौघांचा एक गट झाला. पुस्तकांशी संबंधित चार लेबल्सचा एक गट झाला आणि उरलेले चार एका विजेटमध्ये समाविष्ट केले. ’वेचित चाललो...’ वर डावीकडच्या समासात पुस्तकांसंबंधी सूची तर उरलेले दोन गट उजवीकडच्या समासात समाविष्ट केले आहेत.

ब्लॉगविश्वात मुशाफिरी करत असतात्ना काही ब्लॉग्सवर फोटोंचा स्लाईड-शो पाहण्यात आला. मागे म्हटल्याप्रमाणे ’वेचित चाललो...’ हा प्रथम पुस्तकांतील आवडलेले वेचे संकलित करणे या मर्यादित नि खासगी उद्दिष्ट असलेला ब्लॉग होता. त्यामुळॆ प्रत्येक पोस्ट ही एका पुस्तकाशी निगडित होती. तो फोटोंचा स्लाईड-शो पाहिल्यावर फोटोंऐवजी मुखपृष्ठांचा स्लाईड-शो तयार करुन मुखपृष्ठावर क्लिक केले असता त्या पुस्तकातील वेचे वा त्यासंबंधी लिहिलेले लेखन असलेल्या पोस्ट्स समोर दिसतील अशी सोय करता येईल अशी कल्पना सुचली.

एकप्रकारे ही चित्र-सूची तयार होणार होती आणि वर तयार केलेल्या शब्द-सूचींना पर्याय म्हणून देता येणार होती. थोडक्यात शब्दसूचीमध्ये वर्गीकरणांसाठी वापरलेली एकाहून अधिक टॅब्सची कल्पना आता एकाहुन अधिक इमेजेस अशी बदलून घेतली गेली. शब्द-सूचीमध्ये पुढच्या वर्गीकरणाची सूची पाहण्यासाठी वाचकाला क्लिक करुन टॅब्स बदलावे लागत होते. इथे त्याऐवजी स्लाईड शोचे ’पुढचे’ (Next) किंवा ’मागचे’ (Previous) बटन क्लिक केले की पुढचे मुखपृष्ठ समोर येईल अशी सोय करता येणार होती.

हा पर्याय देणे तुलनेने फार अवघड गेले नाही. ’गुगल डॉक’मध्ये प्रेजेंटेशन्स (पॉवरपॉईंटचा गुगल अवतार) तयार करणे शक्य असल्याने सर्व पुस्तकांची मुखपृष्ठे वापरून तिथे एक स्लाईड शो तयार केला. प्रत्येक मुखपृष्ठाची इमेज अपलोड झाल्यावर एकाच आकारात बदलून घेतली, जेणेकरुन स्लाईड-शो मध्ये अनावश्यक झूम होऊन वेगवेगळ्या आकाराच्या इमेज दिसू नयेत. या प्रत्येक स्लाईडला तुम्हाला हायपरलिंक जोडता येते. प्रत्येक पुस्तकाच्या नावाचे लेबल असल्याने त्या त्या मुखपृष्ठाला त्या लेबलची लिंक जोडून दिली.

यानंतर गुगल तुम्हाला हा प्रसिद्ध करण्याचा(web-publish) कोड तयार करुन देतो. तो फक्त तुमच्या ब्लॉगवर जोडला (मी डाव्या समासात स्वतंत्र विजेटमध्ये वापरला) की काम झाले. सुरुवातीला थोडी अडचण अशी झाली, की त्या स्लाईड-शोला खाली कंट्रोल्सही (Next, Previous, Pause वगैरे) असतात. ते हवे तसे कस्टमाईझ केले तरी गुगल त्याचा रंग वा क्रमवारी बदलून टाकून पंचाईत करे. मग त्याचा कोड थोडा बदलून ते काढूनच टाकले आणि ठराविक वेळाने आपोआप पुढचे मुखपृष्ठ लोड होईल अशी सोय करून ठेवली.

’वेचित चाललो...’ वर लेखनाची एक विशेष वर्गवारी आहे. पुस्तकातील एखादा वेचा निवडताना त्या वेच्याबद्दल, पुस्तकाबद्दल, लेखकाबद्दल किंवा त्या अनुषंगाने जे सुचेल त्याबद्दल लिहित असतो. हे परीक्षण नव्हे, समीक्षा नव्हे की कुठलेही पारंपरिक प्रकारचे पुस्तकाविषयीचे लेखन नव्हे. अमुकच प्रकारे लिहिले पाहिजे असे बंधन मी स्वत:ला घालून घेतलेले नाही. या सार्‍या लेखांचे, पोस्ट्सचे शीर्षक नेहमी ’वेचताना... : <पुस्तकाचे नाव>’ असे दिलेले असते. हे स्वतंत्र लेखन असल्याने यांची पुस्तक वेच्यांहून वेगळी सूची करता आली, तर मला स्वत:लाच अधिक उपयुक्त ठरणार होती. परंतु इथे एका विशिष्ट कारणासाठी मी ’वेचताना...’ ही स्वतंत्र वर्गवारी केलेली नव्हती. त्यामुळे त्यावर आधारित सूची मिळणार नव्हती. त्यामुळे जिथे जिथे शीर्षकामध्ये ’वेचताना...’ दिसेल अशा पोस्ट्सची सूची मला करायची होती. ब्लॉगच्या संपूर्ण सूचीची छाननी करुन त्यांच्या शीर्षकांच्या आधारे निवड करत ही उपसूची तयार करायची होती. पुन्हा प्रथम Javascript चा वापर केला होता. त्याच्या मर्यादा दिसून आल्यावर HTML+CSSचा वापर करुन प्रोग्राम लिहिला आहे.

इतके सारे काम झाल्यानंतर यात्रेच्या सुरुवातीला उल्लेख केलेली समस्या प्रथमच समोर आली. मोबाईल थीममध्ये समासांची आणि पर्यायाने विजेट्सची सोय नसल्यामुळे या सार्‍या सूची फक्त लॅपटॉप/डेस्कटॉपवरच पाहता येतात. आता ही नवी समस्या सोडवण्यासाठी मोबाईल थीममध्ये काही अन्य पर्याय शोधावा लागणार होता.

(क्रमश:)

पुढील भाग >> माझी ब्लॉगयात्रा - ७: मोबाईल-विशेष

माझी ब्लॉगयात्रा - ५ : मजकूर सुरक्षितता

माझी ब्लॉगयात्रा - ४ : ब्लॉग लिहिल्यानंतर << मागील भाग
---

वास्तव आयुष्यात मृत्यू टाळता येत नाही, औषधांनी त्याची संभाव्यता कमी करता येते.
आभासी जगात लेखन-चौर्य टाळता येत नाही, पण त्याची संभाव्यता कमी करता येते.

- स्वामी जिज्ञासानंद

काही वर्षांपूर्वी मी मराठी संस्थळांवर सक्रीय होतो तेव्हाची गोष्ट आहे. माझ्या ब्लॉगला भेट दिल्याचे आणि माझे लेखन आवडल्याचे एका संस्थळमित्राने 'व्यक्तिगत निरोपाने’ (हा संस्थळावरचा खासमखास शब्द) कळवले. मी बुचकळ्यात पडलो. माझा ब्लॉगच नव्हता आणि मी तसा नुकताच लिहू लागलो होतो. दोन-चार बरे लेख या पलिकडे फारसे लिहिलेही नव्हते. त्या लेखनाला आज मी लेखन म्हणू धजणार नाही. फेसबुक पोस्टच्या दर्जाचे ते लेखन म्हणता येईल.

Shutterstock.com येथून साभार.

कुतूहल म्हणून मी शोधले, तर माझा एक लेख असलेला ब्लॉग मला सापडला. गंमत म्हणजे त्या ब्लॉगवर माझ्या परिचयाच्या इतर अनेक मंडळींचे लेख सापडले. (ते माझ्या लेखासोबत असल्याने सारे मीच लिहिले आहेत असा संस्थळमित्राचा गैरसमज झाला होता.) थोडी चौकशी करता हा ब्लॉगमालक भलताच शहाजोग नि उद्धट असल्याचे माझ्या कानावर आले. हे महाशय संस्थळांवरुन, ब्लॉग्सवरुन इतरांचे लेख सरळ उचलून आपल्या ब्लॉगवर चिकटवत असत. लेखकाचे नाव, मूळ लिंक देणे सोयीस्कररित्या टाळून! एखाद्या लेखकाने विचारणा केलीच तर ’मी कुठे म्हणतोय माझा लेख आहे म्हणून. मला आवडलेले लेखन मी फक्त संकलित करतो आहे.’ असा दावा करत. आणि त्याचवेळी हे महाशय पोस्टच्या खाली वाचकांनी केलेल्या कौतुकाचा निर्लज्ज स्वीकारही करत होते. लेखकाच्या निषेधाला उत्तर म्हणून ’उलट मी तुम्हाला जास्तीची प्रसिद्धीच देतो आहे की.’ हा आगाऊपणा आणखी वर ठेवून देई. ’नॅशनल जिओग्राफिक’ने नावाजलेल्या एका फोटोग्राफर मित्राला एका नवथर, चॅनेलपुरस्कृत मासिकाने मानधनाऐवजी ’तुम्हाला प्रसिद्धी देऊ की’ असे निर्लज्ज उत्तर दिले होते. ही तर अगदी अलिकडची, चार-पाच वर्षांपूर्वीची गोष्ट.

दुसरा अनुभव माझा स्वत:चाच. सामाजिक-राजकीय विश्लेषण करणारी एक पोस्ट मी फेसबुकवर टाकली होती. ती अनेकांनी शेअर व फॉरवर्ड केली. लेखन करताना परिच्छेदांचे गणित मी व्यवस्थित सांभाळत असतो. एका महाभागाने शेअर करताना ते विस्कळित झालेले मला दिसले. कुतूहल म्हणून वाचू लागलो तर महाशयांनी त्यात मला अजिबातच अभिप्रेत नसलेली, लेखाची दिशा बदलून टाकणारी, आपल्या मनाची चार वाक्ये घुसडून दिली होती. खाली माझे नाव तसेच ! मी त्यांना याबाबत विचारणा केली असता ’तुमचा मुद्दा स्पष्ट करतो आहे.’ असा दावा त्यांनी केला. म्हटलं, ’बाळा, तुला एकतर मुद्दा कळलेला नाही किंवा माझ्या लेखाच्या पोटात तुझा प्रॉपगंडा घुसडतो आहेस.’

इथे एक मुद्दा मला स्पष्ट करावा लागेल. त्याने माझे लेखन शेअर करुन, त्याला प्रस्तावना म्हणून काही मुद्दे समाविष्ट केले असते आणि ते माझ्या लेखनाशी विसंगत असते, तरीही मी ते समजू शकतो. त्याने ते स्वत:चे आकलन म्हणून लिहिले असते. इथे खाली माझे नाव असल्याने ते मीच लिहिले असा समज होणार होता. त्याला तेच अभिप्रेत होते का मला ठाऊक नाही.

या घटनेनंतर मी ’लेखन/पोस्ट शेअर करायचे तर माझ्या वॉलवरुन लिंकच शेअर करा, कॉपी-पेस्ट नको, भले पोहोच कमी राहिली तरी चालेल’ असा आग्रह धरु लागलो. पण या पलिकडे मला करण्यासारखे फार काही नाही. लेखन मुळातच कॉपी करता येऊ नये अशी तरतूद करणे हाच एकमेव उपाय. पण फेसबुक वा मराठी संस्थळांवर, वृत्तपत्रांच्या वा केवळ ऑनलाईन अस्तित्व असणार्‍या पोर्टल्सवर माझा काडीचाही कंट्रोल नसतो. त्यांनी स्वत:च पुढाकार घेऊन तसे केले असेल तरच मला त्याचा फायदा होऊ शकतो. (टाईम्स गटातील पोर्टल्स काही प्रमाणात हे करतात असे दिसते. कॉपी करण्याचा प्रयत्न केल्यास निवडलेल्या भागापैकी थोडाच भाग कॉपी होतो नि उरलेल्या मजकुराऐवजी साईटचा पत्ता येतो.) त्यामुळे सोपा उपाय म्हणून दीर्घ लेखन करायचे असेल तर मी ते प्रथम ब्लॉगवर लिहून त्याची लिंक फेसबुकवर शेअर करणे सुरू केले.

फेसबुकवर काही मंडळी पोस्ट करताना खाली (c) चिन्ह टाकून आपले नाव लिहितात. यातून कोणताही कॉपिराईट सिद्ध होतो असे मला वाटत नाही. शेअर वा लिंक देण्यापेक्षा पुरी पोस्ट कॉपी-पेस्ट केल्याने अधिक लोकांपर्यंत पोहोचते असा गैरसमज फेसबुकवर पसरलेला आहे. त्यामुळे बरीच मंडळी आवडलेली पोस्ट कॉपी करुन आपल्या वॉलवर पेस्ट करताना दिसतात. या प्रक्रियेत लेखकाचे नाव आपोआप लेखनाबरोबर जाते हा या पद्धतीचा मर्यादित फायदा. त्यामुळे एखाद्या कॉपिबहाद्दराने ते काढून टाकले नि आपलेच लेखन असल्याचा आभास निर्माण केला तर मूळ लेखकाने जाब विचारल्यावर ’तुमचे नाव लिहायचे विसरलो’ अशी मखलाशी करता येत नाही.

ब्लॉगवर आपल्या मजकुराचे रक्षण दोन प्रकाराने करता येते. पहिले म्हणजे कॉपीराईटचा आधार घेणे, आणि दुसरा म्हणजे मुळात तो कॉपीच करता येणारे नाही याची सोय करून ठेवणे.

कॉपीराईट प्रोटेक्शन

भारतात अत्यंत दुबळा असलेला सायबर-लॉ अजून द्वेषमूलक गुन्ह्यांविरोधात पुरेसा परिणामकारक ठरत नाही, तिथे एखाद्या पोस्टच्या मजकुराच्या कॉपिराईट उल्लंघनासाठी तो मदतीला येईल ही शक्यताच नाही. फारतर जिथे आपल्या मजकुराची कॉपी श्रेय न देता कॉपी केलेली दिसेल तिथे जाऊन त्याचा उल्लेख करणे, आपले श्रेय देण्याचा आग्रह धरणे, इतकेच करता येते. पण अडचणीचा मुद्दा असा, की अमुक एका ठिकाणी आपले लेखन कॉपी करुन टाकले आहे, हे कळणार कसे? हे तुम्हा-आम्हाला वैय्यक्तिकरित्या करणे, त्यासाठी सारे वर्ल्ड वाईड वेब शोधत बसणे अशक्यच आहे. त्यासाठी एखाद्या संगणकीकृत सेवेची/सर्व्हिसची मदत मिळाली तरच हे शक्य आहे.

यावर दोन पर्याय आहेत. पहिला म्हणजे ’गुगल अलर्ट’चा(Google Alert) वापर करणे. यात तुमच्या लेखनातील ठराविक, वैशिष्ट्यपूर्ण मजकुराचा भाग हा गुगल अलर्टला देऊन तो कुठेही आढळला की आपल्याला सूचना द्यावी असे सांगून ठेवता येते. (गुगलचे सरपट्टू ऊर्फ Crawlers हे सतत इंटरनेटवर सरपटत माहिती जमा करत राहतात. यात तुमच्या ब्लॉगचीही माहिती आली!) पण हे थोडे जिकीरीचे आहे. कारण तुमच्या लेखनातील अगदी व्यवच्छेदक म्हणावे असे तुकडे तुम्हाला शोधावे लागतात. अन्यथा ते इतर अनेक ठिकाणी वेगळ्या संदर्भात वारंवार येत असतील तर गुगल तुम्हाला सतत सूचना देत राहील आणि त्यातले बहुतेक सगळे फसवे ठरतील. दुसरा पर्याय आहे तो कॉपीसेन्ट्री (Copysentry) सारखी सर्व्हिस वापरण्याचा. ही सर्व्हिस तुमचा ब्लॉग तपासून त्यांच्या पद्धतीने ती माहिती सांभाळून ठेवते. (कुणी हॅशकोड Hashcode किंवा चेकसम checksum हे शब्द ऐकले असतील तर तुम्हाला समजेल) त्यानंतर गुगलप्रमाणेच (बहुधा गुगलच्याच Crawler/ Scrapers वर स्वार होऊन) ते ही इंटरनेटवर ही माहिती शोधत राहतात, नि सापडली की आपल्याला तशी इमेल पाठवतात. या दोनही पद्धतींच्या यशाची संभाव्यता अगदी कमी आहे.

यांच्या वापरात आणखी एक धोका असा, की यासाठी मुळात तुम्हाला तुमच्या ब्लॉगची संपूर्ण फीड या दोन सर्व्हिसेसना खुली करुन द्यावी लागते. आणि एकदा ती खुली केली की स्क्रेपिंगचे (एखाद्या विशिष्ट पानावरचे लेखन खरवडून जमा करत जाणे) थोडे तंत्र अवगत असलेला कुणालाही ती सहज उपलब्ध होते. त्यामुळे एकुणातच हा प्रकार फारसा उपयुक्त नाही असे माझे मत झाले आहे. त्यामुळे आता मजकूर शक्यतो कॉपी करताच येऊ नये याची काळजी घेणे, इतकेच ब्लॉगरला शक्य आहे.

इथे मी मजकुराच्या सुरक्षिततेबाबत बोलतो आहे. तुमचे स्वत:चे असे फोटो वा व्हिडिओ जर तुमच्या ब्लॉगचा भाग असतील, तर त्यांत वॉटरमार्कसारखे काही उपाय वापरून, कॉपीपासून संरक्षण नाही तरी निदान तुमचा ठसा त्यावर राहील याची खातरजमा करुन घेता येते.

कॉपी प्रोटेक्शन

ब्लॉग असो वा कोणतेही संस्थळ/वेबसाईट, त्यावरचा मजकूर कॉपी करण्यासाठी दोन-तीन पर्याय असतात. त्यापैकी पहिला म्हणजे हवा तो मजकूर कम्प्युटरच्या माऊसचा वा की-बोर्डचा वापर करून सिलेक्ट करणे आणि नंतर राईट-क्लिक करुन ’कॉपी’ पर्याय निवडणे किंवा Ctrl+C पर्याय निवडणे. हा पर्याय बंद करणे शक्य आहे. मी वापरलेल्या उपायांना बर्‍यापैकी यश मिळाले आहे.

ब्लॉग ही माझ्या संपूर्ण नियंत्रणातील वेबसाईट वा संस्थळ असते. मला त्यावर स्वत:चे असे कॉपी-प्रोटेक्शन टाकता येते. मी प्रथम एक तयार Javascript कोड विजेट म्हणून टाकला होता. कॉपी करण्याचा प्रयत्न केल्यास तो एक उठवळ (pop-up) मेसेज देऊन तसे न करण्याबद्दल बजावत असे. मोबाईल थीमवर समास/विजेट नसल्याने हा उपाय अर्थातच चालत नसे. हा तसा इतर अनेकांनी वापरलेला कोड होता. पण बहुतेक सर्व ब्राउजर हे आता Pop-up blocker सह येत असल्याने अनेकांना मेसेज दिसत नसे, शिवाय Javascript देखील 'हॅकर्सना सोयीचे' असा निर्णय देऊन अनेक ब्राउजर बंद करुन ठेवत असतात. गुगल क्रोममध्ये Right Click and Copy करण्यासाठी Extensions तयार करुन दिली आहेत. Javascript वापरुन बंद केलेले राईट-क्लिक पर्याय यांच्याद्वारे पुन्हा खुले करून घेता येतात.

त्यानंतर मी HTML+CSS असा एक कोड वापरला, आणि तो विजेटवर वेगळा न ठेवता थेट मूळ थीमच्या कोडमध्येच घुसवून दिला. अर्थात कोणताच उपाय १००‍% बिनचूक नसतो. प्रोग्रामिंगची जाण असलेला त्यातूनही सहज मार्ग काढेल. पण इतके कष्ट करण्याइतके ते लेखन त्याला महत्वाचे वाटत असेल, तर त्याने ते कॉपी करुन जरुर न्यावे असेच मी म्हणेन.

फीड-कंट्रोल

तुमचे लेखन संपूर्णपणे इतरांच्या हातात पडण्याचा अन्य मार्ग म्हणजे ब्लॉगफीड. ब्लॉगरवर ईमेल सबस्क्राईब पर्याय जर तुम्ही वाचकांना दिला असेल, तर तुम्ही नवी पोस्ट लिहिलीत की ती आपोआप ईमेलद्वारे ब्लॉग सबस्क्राईब केलेल्यांपर्यंत पोचते. यातून तुमच्या ब्लॉगवर न येता त्यांना ती वाचण्याची सोय होते. त्याचबरोबर संपूर्ण कंटेंट, कोणत्याही सिलेक्ट+कॉपी पर्याय न वापरता त्यांच्या पदरी पडतो.

एकतर ब्लॉगवर येण्याची तसदी न घेता संपूर्ण लेखन वाचू इच्छिणार्‍यांची सोय पाहावी असे मला वाटत नाही. ’फेसबुक वा व्हॉट्स-अ‍ॅपवर पुरे लेखन टाका तरच आम्ही वाचू’ असा अगोचर आग्रह धरणार्‍यालाही मी वाटाण्याच्या अक्षता लावत असतो. लेखक हा उत्पादक आहे आणि त्याने आपल्या दारी येऊन उत्पादन विकण्याचा आटापिटा करावा ही अपेक्षा मला मान्य नाही. उलट माझे लेखन त्यांना काहीही न गुंतवता, एक पैसा न देता वाचावयास मिळत असेल, तर किमान त्यांनी माझ्या ब्लॉगवर येऊन ते वाचावे, त्यायोगे माझ्या ब्लॉगवरील वावर वाढवावा ही माझी अपेक्षा गैर आहे असे मला वाटत नाही.

यासाठी मला ब्लॉगफीडमध्ये काय द्यावे हे कंट्रोल करण्याचा पर्याय ब्लॉगर देतो. सबस्क्राईब करणार्‍याला संपूर्ण लेख नव्हे, तर केवळ लेखाचा केवळ एक भागच ईमेलद्वारे पाठवण्याचा पर्याय मी निवडतो. यातून नवे लेखन आल्याची सूचना मिळते आणि त्यात काय असावे याचा अदमास घेण्याइतपत मजकूरही. माझ्या मते इतके पुरेसे असते.

तुम्ही ब्लॉग-संग्राहक(blog aggregator) वापरत असाल, तर तुमची नवीन पोस्ट त्यांच्या सूचीत समाविष्ट करताना त्या मजकुरातील एक छोटा भाग ते ही त्यांच्या वाचकांसाठी जोडत असतात. हा तुकडा निवडण्यासाठी त्यांचाही स्वत:चा असा अल्गोरिदम असू शकतो. हा अल्गोरिदम, हा कोड, तुमच्या फीडद्वारे मजकूर घेत असतो. तुमची फीड पुरा मजकूर देत नसेल, तर त्यातून पुन्हा एक तुकडा काढताना कदाचित त्यांना काहीच हाती न लागण्याचा संभव असतो. पण तरीही सूचीमध्ये तुमच्या लेखाचे शीर्षक, ब्लॉगचे नाव दिसत असल्याने या साईड-इफेक्टकडे मी दुर्लक्ष करतो.

बॅक-अप

आपल्या लेखनाची एखादी प्रत सुरक्षित ठेवायची असेल, तर वृत्तपत्रांसह अन्य ऑनलाईन पोर्टल्स, फेसबुकसारखी समाजमाध्यमे यांवर केलेले लेखन तुम्हाला स्वतंत्रपणे आणि हेतुत: उतरवून ठेवावे लागते. संगणकावर वेगवेगळे सांभाळावे लागते. ब्लॉगचा फायदा असा की एकाच बॅक-अप सूचनेत तुमचा संपूर्ण ब्लॉग एका फाईलमध्ये उतरवून घेता येतो. याचा आणखी एक फायदा म्हणजे, ही फाईल अन्य एखाद्या ब्लॉगमध्ये इम्पोर्ट केली, की सर्व पोस्टस मूळ कमेंट वगैरेंसह समाविष्ट होतात. मी जेव्हा ब्लॉगरऐवजी वर्डप्रेसवर शिफ्ट होण्याचा विचार करत होतो, तेव्हा याच पर्यायाचा वापर करुन ब्लॉगरवरील माझे ब्लॉग तिकडे स्थलांतरित केले होते. एका मोठ्या ब्लॉगचे विषयाच्या आधारे एकाहुन अधिक वेगळे ब्लॉग करायचे असतील तर ते ही या पर्यायाचा वापर करुन साध्य करता येते.

मूळ मांडणीमध्ये(Theme) तुमच्या सोयीने - मी केले तसे- काही बदल केले असतील, तर मूळ मांडणीसह प्रत्येक बदलाच्या टप्प्यावरील मांडणीची एक-एक प्रत तुम्हाला तुमच्या संगणकावर वा मोबाईलवर साठवून ठेवता येते. जेणेकरुन बदल करताना काही अनपेक्षित घडले नि ब्लॉगची मांडणी बिघडली, तर सरळ मागची मांडणी पुन्हा आणून ब्लॉगची गाडी मूळपदावर नेता येते. माझ्या काही फसलेल्या प्रयोगातून सावरण्यासाठी मला याचा उपयोग झाला.

(क्रमश:)

पुढील भाग >>माझी ब्लॉगयात्रा - ६ : अनुक्रमणिका आणि सूची

माझी ब्लॉगयात्रा - ४ : ब्लॉग लिहिल्यानंतर

मागील भाग << माझी ब्लॉगयात्रा - ३ : ब्लॉग लिहिताना
---

ब्लॉग तयार केल्यानंतर, ब्लॉगपोस्ट लिहिल्यानंतर बहुतेक ब्लॉगर मंडळी ’प्रसिद्ध करा’ (Publish) पर्याय वापरतात नि थांबतात. याच्यापुढे काही असते याची बहुतेकांना माहिती नसते. काही मंडळी तर इतकी बेफिकीर दिसतात, की त्यांच्या एकाच पोस्टमध्ये वेगवेगळ्या आकाराचा वा प्रकाराचा फॉन्ट असणारा मजकूर दिसतो. अन्य एडिटरमधून किंवा अन्य वेबसाईटवरून पेस्ट करताना त्याच्या फॉरमॅटिंगचे काय होते, याबाबत बहुतेक सारे अनभिज्ञ असतात. बरं निदान समोर वेगवेगळे फॉन्ट दिसत असताना ते सुधारून कसे घ्यावे याचा विचार तरी करावा. यातील काही मंडळी तर पोस्ट प्रसिद्ध केल्यावर ती पोस्ट, आपला ब्लॉग, निदान आपल्या ब्राउजरवर व्यवस्थित दिसते का, याची शहानिशाही करत नसावेत असा मला दाट संशय आहे. (जसे फेसबुकवर शेअर बटन दाबल्यावर आपली वॉल पाहून आपल्याला अपेक्षित तेच शेअर झाले का याची शहानिशा करत नाहीत तसे.)

आणखी एक मुद्दा असतो वाचणार्‍याला दिसणार्‍या मांडणीचा. पहिली महत्वाची गोष्ट म्हणजे जसे लेखकाला दिसते नेमके तसेच वाचकाला दिसेल याची शाश्वती देता येत नाही! विविध संस्थळे, ब्लॉग, पोर्टल्स ज्याच्यामार्फत आपण उघडतो त्या ब्राउजरची गंमत अशी असते की, आपल्या संगणकावर -समजा- गुगल क्रोममध्ये आपण एखादी संस्थळ/वेबसाईट जशी दिसते तशीच ती फायरफॉक्स, त्याची भावंडे आईसड्रॅगन वा वॉटरफॉक्स, क्रोमची भावंडे कोमोडो ड्रॅगन आणि ब्रेव्ह ब्राउजर, किंवा या दोनही कुटुंबांपलिकडे असलेल्या मायक्रोसॉफ्टचा एज किंवा ऑपेरा ब्राउजरवर दिसत नाही. तुम्ही तुमच्या लेख/बातमीमध्ये समाविष्ट केलेल्या मजकुरासह इतर स्वरुपातील माहितीचा परस्परसंबंधच काय तो ब्राउजरला सांगितलेला असतो. (चित्राच्या उजवीकडे अमुक अंतरावर मजकूर सुरु करणे. एकुण स्क्रीनच्या डाव्या वा उजव्या बाजूस इतके टक्के भाग हा अमुक चित्राने राखून ठेवणे वगैरे) त्यापलिकडे प्रत्येक ब्राउजर आपापल्या पद्धतीने मजकुराची मांडणी करत असतो. यात थोडे डावे उजवे होत जाते.

क्रोमवर एखाद्या ग्राफच्या बरोबर शेजारी दिसणारा मजकूर ऑपेरामध्ये थोडा खाली अथवा वर सरकलेला दिसून येतो. त्यामुळे वाचकाला दिसणार्‍या मजकुराचा पोत बदलतो. याशिवाय तुमच्या डेस्कटॉप/ लॅपटॉप/ टॅब/ मोबाईलच्या प्रणालीमध्ये (विंडोज/ अ‍ॅंड्रॉईड/ लिनक्स/ क्रोमिअम वगैरे) फॉन्टचा ठरवून दिलेला आकार (small, median, large वा custom), तुमच्या ब्राउजरमधला फॉन्ट, एन्कोडिंगची तुम्ही वा तुमच्या ब्राउजरने तुमच्यासाठी निवडलेली पद्धत, आदी गोष्टींवर समोर दिसणार्‍या पानाची मांडणी बदलत जाते. ब्राउजरमध्ये साधे झूम-इन/झूम-आउट केले तरी इमेज आणि मजकुराचे गुणोत्तर बदलत जाते.

मोबाईल, टॅब, डेस्कटॉप यांच्यासाठी ब्लॉगची मांडणी वेगळी असते हा आणखी एक अडचणीचा मुद्दा. याशिवाय ओळ संपताना तिथे आलेल्या शब्दाच्या रुंदीनुसार तो त्याच ओळीत प्रकाशित होईल की नव्या ओळीत जाईल हे ठरते. झूम, फॉन्ट्चा आकार वगैरे मुळे याचे स्थान खाली अथवा वर होत जाते.

पोर्ट्रेट मांडणी.

लॅंडस्केप मांडणी.

उदाहरण घ्यायचे तर हा एक ताजा ब्लॉग पाहा. एकाच मोबाईलवर पोर्ट्रेट आणि लॅंडस्केप मोडमध्ये याची मांडणी कशी दिसते पाहा. ही मांडणी मजकुरापेक्षा फोटोला अधिक महत्व देणारी आहे. काहींना ती सोयीची वाटेल. याउलट माझी मांडणी दोन्हीकडे सारखीच दिसेल, परंतु पोर्ट्रेट मोडमध्ये इमेज कदाचित पुरेशी मोठी दिसणार नाही. दोन्हींचे फायदे-तोटे आहेत, पण मी दुसरी मांडणी स्वीकारली आहे कारण 'वेचित चाललो...’ वर पुस्तकांबद्दल लिहिताना मला ती अधिक सोयीची वाटली आहे.

या समस्यांमुळे ब्लॉग तयार झाल्यानंतर किमान एकदा, आणि जर पोस्टमध्ये स्वत:चे असे फॉरमॅटिंग वापरत असलात तर प्रत्येक पोस्टनंतर, आपला ब्लॉग वेगवेगळ्या ब्राउजरवर कसा दिसतो, हे - निदान आपल्या संगणक/टॅब/मोबाईलवर तपासून पाहणे आवश्यक ठरते. मी वर उल्लेख केलेले पाच-सहा ब्राउजर तपासून पाहात असतो.

Photo: Castle Apple Orchard in Madrid, Spain.

आयफोन वा एकुणात अ‍ॅपलधारी म्हणजे सात खंदक, सात तट आणि सतराशे सैनिक यांच्या गराड्यात बसून ’तुम्ही हल्ली भेटत नाही हो.’ अशी दांभिक तक्रार करणार्‍या शेजार्‍यासारखे असतात. हे स्वत:ला संगणक आणि मोबाईल विश्वातले उच्चभ्रू समजत असतात. मध्यंतरी अशाच एका ’अ‍ॅपलस्टिल्टस्किन’ मित्राने माझ्या ब्लॉगमधील व्हिडिओ आपल्याकडे नीट दिसत नाही अशी तक्रार केली. मी पाचही ब्राउजरवर चेक केले असल्याने बुचकळ्यात पडलो. अगायायायायफोन ही माझी पोस्ट आठवली, आणि अचानक ट्यूब पेटली. त्याला विचारले, ’बाबा ब्राउजर कुठला वापरतोस?’ यावर अपेक्षित उत्तर आले सफारी, आणि अर्थातच आयफोनवर.

आता सफारीवर ब्लॉग टेस्ट करू म्हणून तो डाऊनलोड करण्यास शोधाशोध केली तर असे दिसले, की २०१२ नंतर अ‍ॅपल महाशयांनी विंडोजवर हा ब्राउजर देणे बंदच केले आहे. इतकेच नव्हे तर हा ब्राउजर ज्या WebKit ब्राउजर-एंजिनवर तयार केला आहे ते एंजिन अ‍ॅपलची iOS प्रणाली वगळता इतर कोणत्याही प्रणालीवर चालत नाही (not supported). म्हणजे समजा (हे येरागबाळ्याचे आणि गरीबाचे काम नोहे. पण तरीही...) ते घेऊन विडोज वा अ‍ॅंड्रॉईडवर स्वत:च ब्राऊजर तयार करुन त्यावर टेस्ट करेन म्हटले तरी तो पर्यायही उपलब्ध नाही. थोडक्यात आमचा ब्लॉग आयफोनधारी उच्चभ्रूंना कसा दिसतो हे पाहण्यासाठी आम्हालाही सक्तीने आयफोन किंवा आयपॅड किंवा अ‍ॅपल लॅपटॉप घ्यावा लागणार.

म्हटलं ही त्यांची सात तळ्याची तांब्या-पितळेची माडी त्यांची त्यांना लखलाभ असो. ’अ‍ॅपलवर, अ‍ॅपलवाल्यांसाठी, अ‍ॅपलवाल्यांनी बनवलेली/चालवलेली वेबसाईट’च त्यांनी पाहावी असा फुकटचा सल्ला देऊ इच्छितो. मित्राला म्हटले, "तू आमच्या गावकुसाभाईर बंगला बांधून बसलाईस. गावात ये. मग तुपली-मपली वळखपाळख नीट व्हईल. तंवर माझं ग्रेट लिखान* तुला नीट दिसत न्हाई, वाचता येत न्हाई, ह्ये तुजं दुर्दैव रं माज्या बाबा." (*माज काय फक्त अ‍ॅपलवाल्यांनीच करावा की काय.) अर्थात पुढे व्हिडिओ समाविष्ट करण्यासाठी (video embedding) मी जे तंत्र वापरले त्याने सफारीवरही समस्या दूर झाली असे समजले.

हे वाचून अनेक ब्लॉगरही बुचकळ्यात पडले असतील. म्हणतील, ’आमचे व्हिडिओ/फोटो तर नीट दिसतात बुवा. यालाच का अडचण येते?’ त्याचे उत्तर असे आहे की तुम्ही व्हिडिओ हे बव्हंशाने मजकुराहून वेगळे, स्वतंत्र परिच्छेद म्हणून समाविष्ट करत असता. मला व्हिडिओ/फोटो आणि त्याच्याशी सुसंगत मजकूर एकमेकांशेजारी हवा असतो. यामुळे कोणतीही प्रणाली वा ब्राउजर असेल तर माझ्या मजकुराची मांडणी शक्यतो एकसारखी राखता येते.

तसा तो ठेवताना दोन अडचणीचे मुद्दे येतात. पहिला, मजकूर म्हणजे शब्द आणि फोटो/व्हिडिओ यांच्या आकारबदलाच्या गणितामध्ये मोठा फरक आहे. त्यामुळे झूम केले किंवा मोबाईलवर पोर्ट्रेट मोडमधून लॅंडस्केप मोडमध्ये गेले, की त्यांचा परस्परसंबंध बिघडतो. वेगवेगळ्या ब्राउजरवर पडणारा फरक तर आहेच. विशेषत: मोबाईलवर याबाबत अनेक समस्या येतात. स्वतंत्र परिच्छेदात फोटो/व्हिडिओ असतील तर ही समस्या येत नाही.

दुसरा मुद्दा म्हणजे डेस्कटॉप/लॅपटॉप, टॅब, मोबाईल यांच्यासाठी वेगवेगळ्या थीम्स (मांडणी) असतात. मोबाईलच्या लहानशा स्क्रीनचा विचार करुन ज्याला lightweight म्हणतात तशा स्वरूपाची मांडणी त्याच्यासाठी असते. तुमचा ब्लॉग जसा मोबाईलवर दिसतो तसा टॅबवर दिसत नाही, आणि जसा टॅबवर दिसतो तसाच लॅपटॉपवर दिसेल याची खात्री देता येत नाही. अनेकदा फोटो वा व्हिडिओ मोबाईल स्क्रीनच्या रुंदीची मर्यादा झुगारून जाताना दिसतो. (निदान ब्लॉगरमध्ये) ब्लॉग तयार झाल्यावर या तीनही उपकरणांवर कसा दिसेल याचे पूर्वावलोकन (preview) वेगवेगळे पाहता येतात. त्यानुसार आवश्यक त्या दुरुस्त्या कराव्या लागतात. आणि रिकामी जागा (white space) वा मोकळी ओळ (line) सोडून हे नेहमीच साधत नाही.

मोबाईलच्या मर्यादा

stackoverflow.com येथून साभार

मोबाईलचा स्क्रीन संगणकाच्या पडद्याहून बराच लहान असतो. लॅपटॉप वि. मोबाईल स्क्रीनचे जे गुणोत्तर असेल तेच जर त्यावरील फॉन्टमध्येही नेले, तर लॅपटॉपवरील मांडणी मोबाईलवर तंतोतंत तशीच दिसू शकेल... भिंग लावून पाहिली तर! कारण त्याचा फॉन्ट माणसाच्या डोळ्याला वाचताच येणार नाही. म्हणून ब्लॉगर (आणि इतर बहुतेक संस्थळे/वेबसाईट्सही) मोबाईल थीम ही डेस्कटॉप थीमहून वेगळी ठेवतात. मोबाईल थीम ही अधिक सुटसुटीत असते, आणि म्हणून त्यावर मर्यादितच पर्याय उपलब्ध असतात.

मी ’वेचित चाललो...’ हा ब्लॉग चालू केल्यानंतर एका फेसबुक-मैत्रिणीने एका लेखावर कमेंट करुन ’या ब्लॉगवर नवीन लेखन येईल तेव्हा त्याची सूचना मला मिळावी म्हणून काय करता येईल?’ असा प्रश्न विचारला होता. त्यावर ब्लॉगवर गुगलचे ’सबस्क्राईब’ आणि ’फॉलो-बाय-ईमेल’ विजेट असे दोन पर्याय दिले आहेत, असे मी कळवले होते. पण तिने सबस्क्राईब केल्याचे दिसले नाही. काही दिवसांनंतर अन्य एका मित्राने माझ्या लेखातील काही भाग कॉपी करुन एका व्हॉट्स-अ‍ॅप चॅटमध्ये उद्धृत केला होता. मी कॉपी प्रोटेक्शन लावलेले असल्याने त्याला हे कसे जमले असावे, असा प्रश्न मला पडला. त्याने मोबाईलवरुन कॉपी केल्याचे सांगितल्यावर मी शोध घेतला. मी केलेले कॉपी-प्रोटेक्शन मोबाईल थीमवर चालत नाही असे लक्षात आले. तेव्हाच ही ट्यूबही पेटली, की सबस्क्राईबबाबत प्रश्न विचारणारी व्यक्ती मोबाईलवरुन ब्लॉग पाहात असेल, तर तिला सबस्क्राईब पर्याय - आणि इतर कोणतेही विजेट - दिसतच नसणार. त्यामुळे तो पर्यायच तिला उपलब्ध नसेल. मी स्वत: मोबाईलवर ब्राउजिंग, व्हॉट्स-अ‍ॅप वगैरे क्वचितच वापरतो. माझी सारीच कामे ही लॅपटॉपवर होत असल्याने मी मोबाईलकडे फार लक्षच दिले नव्हते.

मोबाई्लच्या थीम्स (मांडणी) या समासांचा म्हणजे कॉलम्सचा वापरच करत नाहीत. एखाद्या अनुक्रमणिकेसारखी लेखांची सूची देऊन मोकळ्या होतात. त्यामुळे सर्वस्वी मोबाईलवर अवलंबून असणार्‍या मंडळींना सर्वात अलीकडचे लेखन वगळता जुने लेखन वाचण्याची कुठलीही सोय राहात नाही. (लॅपटॉपवर ब्लॉग-सूची दिसत असल्याने ते सुलभ होते). आता मोबाईल वापरणार्‍यांना सूची द्यायला जागाच नाही. मग पुरी सूची नाही, निदान प्रत्येक लेखासोबत आणखी एखाद्या लेखाची शिफारस करता आली, तर लेखांची साखळी तयार होईल. ती वाचकांनसाठी आणि पर्यायाने ब्लॉगच्या प्रसिद्धीसाठीही उपयुक्त ठरेल असे माझ्या ध्यानात आले. ते पुढे मी समाविष्ट केलेही (कसे ते पुढे येते आहे.) त्याचबरोबर मोबाईलवर सबस्क्राईब पर्याय उपलब्ध करुन देणे आवश्यक होते. त्यासाठी मोबाईल थीममध्ये बदल करणे आवश्यक ठरले. म्हणजे आता ब्लॉगरच्या प्रोग्राममध्ये/कोडमध्ये ढवळाढवळ अनिवार्य ठरली.

मी स्वत: सुमारे दहा वर्षे सॉफ्टवेअरमध्ये अगदी संकल्पनेपासून ते चाचणी (आणि आज अस्तंगत झालेली संकल्पना म्हणजे User Manual) पर्यंत सर्व कामे केलेली असल्याने प्रोग्रामिंगवर चांगली पकड आहे. पण तेव्हा आम्ही प्रामुख्याने C आणि त्याच्या C++ सारख्या भावंड-भाषांमध्ये, म्हणजे संगणकाच्या पायाच्या स्तरात काम करत होतो. आता ब्राउजर नि मांडणी यांच्यासाठी HTML, CSS तसंच Javascript अशा पृष्ठ-स्तरातील भाषांमध्ये काम करावे लागले. त्यामुळे सुरुवातीला थोडे अडचणीचे गेले हे कबूल करतो. सुदैवाने ब्लॉगरची (blogspot.com चा आश्रयदाता blogger.com) कम्युनिटी अतिशय जागरुक(vibrant) असल्याने बरेच माहिती, विजेट्स तयार मिळतात. कम्युनिटीवर प्रश्न देऊन आपल्या समस्येचे उत्तर विचारता येते. माझ्या तंत्र वापरात, प्रोग्रामिंगमध्ये निम्मा वाटा या ब्लॉगर कम्युनिटीचा आहे हे नमूद करायला हवे.

(क्रमश:)

- oOo -

पुढील भाग >> माझी ब्लॉगयात्रा - ५ : मजकूर सुरक्षितता

माझी ब्लॉगयात्रा - ३ : ब्लॉग लिहिताना

मागील भाग << माझी ब्लॉगयात्रा - २ : माझी वाटचाल
---

(हा भाग सामान्य तयारीचा आहे. ज्यांना ब्लॉग सुरु करायचा आहे पण त्याबाबत अजिबात माहिती नाही अशांना अधिक उपयुक्त. मी स्वत: ब्लॉगर वापरत असल्याने इथे स्क्रीनशॉट्स त्याचे दिले आहेत.)

सर्वात प्रथम तुम्हाला स्वत:चा असा ब्लॉग पत्ता तयार करावा लागेल. त्यासाठी तुम्हाला ब्लॉगचे नाव निश्चित करुन त्यानुसार पत्ता तयार करता येईल. उदा. रमताराम या टोपणनावाने मी संस्थळावर लेखन करत असल्याने ’रमतारामाचे विश्रांतीस्थळ’ हे माझ्या ब्लॉगचे नाव निवडले आणि म्हणून ramataram हा माझा ब्लॉग पत्ता निश्चित केला.

आता हा ब्लॉग तयार करण्यासाठी मी प्रथम ब्लॉगर.कॉम (किंवा तुमचा ब्लॉगसेवादाता जो असेल तो) वर लॉगिन केले. (गुगलचा फायदा - आणि कदाचित तोटाही - हा की एकदा गुगल लॉगिन केले की ब्लॉगरवरही तुम्ही लॉगिन होता.) आता मी draft.blogger.com वर पोचलो. इथे मी माझा ब्लॉग तयार करणार आहे.

स्क्रीनशॉट पाहिला तर माझे सध्या तीन ब्लॉग दिसतात नि खाली New Blog... पर्याय आहे. त्यावर क्लिक करुन तुम्ही नवा ब्लॉग तयार करता येईल. (तुम्ही सुरुवात कराल तेव्हा वरची यादी अर्थातच कोरी असेल.) त्यात तुम्हाला शीर्षक (माझे: ’रमतारामाचे विश्रांतीस्थळ’ ) आणि पत्ता (माझा: ramataram.blogspot.com) द्यावे लागतील. आता तुमचा ब्लॉग तयार (create) झाला.

पूर्वतयारी

ब्लॉग तयार केल्यानंतर पहिला टप्पा असतो येतो ’ब्लॉगर’, वर्डप्रेस वा तुम्ही निवडलेल्या अन्य ब्लॉगमंचाच्या अखत्यारित येणारे पर्याय निवडण्याचा. ब्लॉगची थीम अर्थात एकुण जडणघडण ही ब्लॉग सुरू करताना केलेली पहिली निवड असते.

ब्लॉगर असो वा अन्य सेवादाते ते काही फ्री थीम्स अथवा बांधणीची प्रारूपे तुम्हाला देऊ करतात. (उजवीकडे 'Customize' बटणाच्या खाली पाहा.) या सोप्या बांधणीपैकी एखादी कमी गुंतागुंतीची थीम निवडून सुरुवात करता येईल. यासाठी ’Theme’ वर क्लिक केल्यावर उजवीकडे काही थीम्स दिसतात त्यापैकी एक निवडून तुमच्या ब्लॉगला लागू (apply) करावी. या निवडीला मदत व्हावी यासाठी तिथे Previewची सोय आहे.

एकदा हवी ती थीम निवडली की Customize बटन दाबून थीमसाठी विविध पर्याय मिळतीलया थीममध्ये विविध मगदुराच्या मजकुरासाठी फॉन्ट्सची निवड, रंगांची निवड हा पहिला टप्पा. ब्लॉगच्या शीर्षकासाठी, पोस्टच्या शीर्षकासाठी, पोस्टच्या तारखेसाठी, मुख्य मजकुरासाठी... फॉन्ट निवडण्याचे पर्याय तुम्हाला मिळतात. तुमच्या नजरेला ते पुरेसे आकर्षक वा समाधाकारक दिसतील अशी निवड तुम्ही करु शकता. त्याचबरोबर शीर्षक पार्श्वभूमी, पोस्टची पार्श्वभूमी, ज्यांना विजेट किंवा अ‍ॅड-ऑन्स म्हणतात, अशा सुट्या पण पूरक चौकटींची पार्श्वभूमी, त्यांची सार्‍यांची शीर्षके आदि विविध जागी वापरल्या जाणार्‍या रंगांची निवड करता येते. हा सारा मजकुराच्या बांधणीचा अर्थात थीम (Theme) भाग झाला.

यातील Adjust Widths या पर्यायामध्ये तुम्हाला ब्लॉगची एकुण रुंदी, समासांची रुंदी निश्चित करता येईल, तर Advanced पर्यायामध्ये रंग, फॉन्ट वगैरे निश्चित करता येईल. तुम्हाला हवी ती रंगसंगती आणि फॉन्ट निवडला की उजवीकडे ताबडतोब दिसेल. तो समाधानकारक दिसला की आपली निवड करुन पुढे जाता येईल.

महत्त्वाचे: इथे दिसणारे पर्याय तुमच्या सुरुवातीच्या थीमच्या निवडीनुसार वेगळे असू शकतात. परंतु ब्लॉगची रुंदी, रंग नि फॉन्ट हे मात्र सर्वच थीम्समध्ये निवडता येतात. काही थीम्स तुमच्या विजेट्स अथवा गॅजेट्ससाठी देखील काही बदलांची मुभा इथे देऊ शकतात.)

तुमच्या ब्लॉगवर तुम्ही लिहिता त्या पोस्ट्सखेरीज अन्य काही गोष्टी समाविष्ट करणे वाचकाच्या दृष्टीने उपयुक्त ठरते. या अत्यावश्यक नसल्या तरी उपयुक्त असतात. त्यात ब्लॉगमध्ये समाविष्ट असलेल्या पोस्टची सूची, विषयवार वर्गवारी, तुमचा ब्लॉग इतरांना सबस्क्राईब करण्याचा पर्याय, लेखकाबद्दल थोडी माहिती अशा काही वरकड गोष्टींचा समावेश होतो. तुमच्या ब्लॉगमधीन लेखनाची जातकुळी ध्यानात घेऊन आणखी काही उपयुक्त गोष्टी इथे देता येतात. हे सारे सामान्यपणे ज्यांना विजेट (widget) किंवा गॅजेट (Gadget) म्हटले जाते त्यांच्या स्वरूपात दिले केले जाते. आणि हे प्रामुख्याने स्तंभ अथवा कॉलममध्ये समाविष्ट होते.

त्यामुळे आता मांडणीचा(Layout) विचार करावा लागतो. यात ब्लॉगमधील पोस्ट्स एकाशेजारी एक दिसणार्‍या टाईल्ससारख्या दिसाव्यात की एकाखाली एक, समास एक असावा की दोन, एक असला तर डावीकडे असावा की उजवीकडे, ब्लॉगरील पोस्टची यादी कशा स्वरूपात दाखवावी, वर्गीकरण (categories/ tags) कशा दाखवावे वगैरेंची निवड येते. वरील तीन पर्यायांपैकी दोन आपण आधीच वापरले आहेत. आता मधला, म्हणजे Layout हा पर्याय वापरला जाईल.

या पर्यायांपैकी काही पर्याय हे तुम्ही सुरुवातीला निवडलेल्या थीमवर अवलंबून राहतील. उदाहरणार्थ तुम्ही जर समोर एकाखाली एक अशा सर्व पोस्ट दाखवणार्‍या थीमऐवजी एकाशेजारी एक चौकटींच्या () स्वरूपात पोस्टस दाखवणारी थीम निवडली असेल तर इथे समासांचे काही पर्याय उपलब्ध असणार नाहीत. यासाठी थीमची निवड प्रथम आणि मांडणी त्यानंतरच करावी लागेल. मांडणीची निवड केल्यानंतरही पाहून ब्लॉग आपल्या अपेक्षेप्रमाणे दिसतो का याची खातरजमा करुन घेणे गरजेचे असते.

वर आपण थीमशी संबंधित रंग, फॉन्ट वगैरेंच्या निवडीसाठी Customize बटण दाबून पुढे गेलो होतो. पण तिथे दिलेल्या पर्यायांपलिकडे तुम्हाला बदल करता येत नाहीत. त्या पलिकडे अनेक गोष्टी थीमचा भाग असतात. त्या बदलण्यासाठी तुम्हाला प्रोग्रामिंग अथवा कोडिंगचा आधार घ्यावा लागतो. या पर्याय फक्त प्रोग्रामिंगबाबत पुरेशी माहिती असणार्‍यांनीच वापरावा. कारण थीम आणि मांडणी हे तुमच्या पोस्टच्या मजकुरासह अखेरीस एकत्र होऊन ब्राउजरमध्ये येत असल्याने, एका भागात झालेली चूक पुढे इतरा विभागातही अनपेक्षित परिणाम घडवू शकते. तुम्ही प्रोग्रामिंगचा वापर करु इच्छित असाल तर Customize बटणालगत असलेले त्रिकोणी बटण दाबले तर Edit HTML हा पर्याय मिळत. त्याचबरोबर थीमचा बॅक-अप आणि मोबाईलसाठी असलेल्या वेगळ्या थीममध्ये बदल करण्यास काही मोजके पर्यायही उपलब्ध होतात. प्रोग्राम अथवा कोडमध्ये बदल करु इच्छिणार्‍यांनी Edit HTML या पर्यायाचा वापर करावा.

पुढच्या टप्प्यात ब्लॉग-सेटिंग्स निवडायची आहेत. या ब्लॉगचे शीर्षक (माझे ’रमतारामाचे विश्रांतीस्थळ’), भाषा निवडता येते. मी मराठी निवडली असल्याने दिनांक, वार, अनेक विजेट्सची शीर्षके (उदा. category ऐवजी वर्गवारी) तळाशी Author ऐवजी लेखक...वगैरे थीमशी संबंधिक बहुतेक मजकूर हा मराठीमध्ये दिसू लागतो.

याशिवाय तुम्हाला ब्लॉगचे संपादक आणि लेखक कोण याची निवड करता येते. एका ब्लॉगवर एकाहुन अधिक व्यक्ती लेखन करु शकतात. हे सर्व लेखक म्हणून समाविष्ट होतात. तर ब्लॉगचा संचालक हा संपादक म्हणून राहतो. याशिवाय लेखनामध्ये काही भाग केवळ सज्ञान व्यक्तींसाठी असेल तर असे लेखन त्यानुसार वर्गीकृत करता येते आणि सेटिंगमध्ये असे लेखन वाचण्यासाठी वयाचे निर्बंध घालता येतात.

तुमचे स्वत:चे असे संस्थळ नाव (उदा. www.ramataram.com) खरेदी केले असेल ते नाव तुमच्या ब्लॉगला पर्यायी नाव म्हणून जोडता येते. जेणेकरुन कुणी त्या संस्थळाला भेट देण्याचा प्रयत्न केला तर त्यांची वाट वळवून तुमच्या या ब्लॉगवर आणून पोहोचवली जाते. म्हणजे स्वतंत्रपणे विकसित न करता, त्यासाठी जागा (storage) विकत न घेता, तुमचे संस्थळ चालू होते. या खेरीज तुमच्या पोस्टस कुणाला दिसाव्यात, त्यावर कुणाला टिपण्णी (comment) करता यावी (किंवा कुणाला करता येऊ नये) काही मंडळी प्रोग्रामद्वारे तुमच्या ब्लॉगवर ढवळाढवळ करु नयेत म्हणून कॅप्चा (Captcha) नामे संरक्षक टप्पा असावा की नसावा, ईमेलद्वारे लेखकांना लेखन थेट पोस्ट करता यावे की नाही, वाचकांनाही ईमेलद्वारे कमेंट पाठवता याव्यात की नाही... असे अन्य पर्यायही निवडता येतात.

यात एक महत्वाचे सेटिंग आहे ते फीडचे (Site Feed). याकडे बहुधा दुर्लक्ष केले जाते. पण तुमच्या मजकुराची सुरक्षिततेला तुम्ही महत्त्व देणार असाल, तर हे सेटिंग तुमच्या दृष्टीने महत्वाचे आहे. तुम्ही सबस्क्राईब पर्याय देणार असाल, तर इथे काळजी घेणे गरजेचे आहे. नव्या पोस्टच्या सूचनेबरोबर त्यातील मोजकाच मजकूर ईमेलद्वारे पाठवला जाईल याची काळजी इथे घेता येते.

या पलिकडे ब्लॉगवर किती पाने (Pages) असावीत याची निवडही करता येते. सुरुवात करताना कुठल्याही मांडणी(Theme) मध्ये ’मुख्यपृष्ठ’(Main Page) या नावाचे एक पान तयार असते. या पलिकडे आवश्यक वाटल्यास आणखी पाने तयार करता येतात. मला स्वत:ला या पर्यायाची उपयुक्तता फारशी समजली नाही. त्याऐवजी मी ’लेबल’ अथवा वर्गवारीचा वापर करुन, त्यातील मोजकी लेबल ही मांडणीत वरच्या बाजूला पृष्ठांप्रमाणे जोडली आहेत..

लेखन आणि लेखनसाहाय्य

ब्लॉगचा मुख्य भाग म्हणजे पोस्ट जी प्रामुख्याने लेखन स्वरूपात असते. त्यातही माफक फॉरमॅटिंग करण्यास ब्लॉगरने (आणि इतर ब्लॉगमंचांनी) वाव ठेवला आहे. त्यापलिकडे तुम्हाला HTML टॅग वापरण्याची माहिती असेल, तर बरेच अधिक स्वातंत्र्य घेता येते. पण ते पुढे तांत्रिक मुद्द्यांसंदर्भात येतेच आहे. साधारणपणे फॉंट्चा प्रकार, आकार, वजन (बोल्ड, तिरपा ठसा, अधोरेखा वगैरे) वगैरे सोबतच शीर्षक, उपशीर्षकांसाठी वेगळ्या फॉरमॅटिंगची सोय आहे. शब्दांचा रंग आणि मजकुराच्या पार्श्वभूमीचा रंगही मोजक्या पर्यायांतून निवडता येतो. एखाद्या शब्दाला वा शब्दसमूहाला अधिका महितीसाठी संदर्भ म्हणून हायपरलिंकही (hyperlink) जोडता येते. माझ्या मते सर्वसाधारण ब्लॉगलेखकांसाठी इतके पुरेसे होते.

मायक्रोसॉफ्ट वर्ड वा तत्सम बाह्य एडिटरमध्ये तुम्ही मजकूर तयार करुन पोस्टच्या एडिटरमध्ये पोस्ट केला तर दोन एडिटर्समधील सेटिंगमधील फरकामुळ पोस्टची मांडणी बिघडू शकते. ब्लॉगरमध्ये हे टाळण्यासाठी बाहेरून पेस्ट केलेला मजकूर सिलेक्ट करुन ’रिमूव्ह फॉरमॅटिंग’ पर्यायाचा वापर करावा. पोस्ट संपादकाच्या (Editor) मेन्यूच्या शेवटी ’...’ दिसतात. ते क्लिक केल्यावर काही जास्तीचे पर्याय दिसू लागतात. या इंग्रजी T हे अक्षर आणि त्याला खोडणारी तिरपी रेष दिसते. हे बटण दाबून निवडलेल्या मजकुराचे फॉरमॅटिंग काढून टाकता येते.

त्या पलिकडे तुम्हाला पोस्ट बनवण्यासाठी स्वत:ची अशी templates वा आराखडे तयार करुन समाविष्ट करता येतात. उदा. कवितेची पोस्ट करण्यास एक आराखडा तर गद्य पोस्टसाठी दुसरा वापरता येऊ शकतो. असे एकाहुन अधिक आराखडे तुम्ही थीममध्ये साठवून ठेवले असतील, तर नवी पोस्ट तयार करताना त्यातील एक निवडता येतो. मी स्वत: कवितेसाठी एक आराखडा तयार करुन ठेवला आहे तर पुस्तकातील वेच्यांसाठी, त्या अनुषंगाने केलेल्या लेखनासाठी दुसरा आहे. अर्थात यासाठी तुम्हाला प्रोग्रामिंगची प्राथमिक माहिती हवी. नसेल तर इथे पास द्यावा.

आपण वृत्तपत्रे वाचतो, तेव्हा पुरवणीमधील अनेक लेखांसोबत तसंच मुख्य प्रतीमधील अनेक बातम्यांसोबत फोटो, रेखाचित्रे असतात. यात काही थेट मजकुराशी संबंधित असतात (उदा. बातम्यांसोबत असणारे एखाद्या कार्यक्रमाचे फोटो) तर काही प्रातिनिधिक, मुद्दा अधोरेखित करण्यासाठी जोडलेले असतात. अनेकदा सलग लेखन हे कितीही उत्तम असले, तरी त्यात एकप्रकारचे एकारलेपण (monotony), कंटाळवाणेपण येत जाते. त्यामुळे सोबत जोडलेले फोटो वा रेखाचित्रे कंटाळवाण्या प्रवासात रस्त्यावर दिसणार्‍या रंगीबेरंगी जाहिरातफलकांसारखे काम करतात. डोळ्यांना जागे ठेवतात.

लेखन पुरे झाल्यावर त्याला सुसंगत अशी चित्रे, फोटो, रेखाचित्रे, भाष्यचित्रे शोधणे हा पहिला टप्पा असतो. अनेकदा असे होते, की अशा इमेजेस सापडतात, पण त्यावर वॉटरमार्क टाकून व्यावसायिक वापरासाठीच राखून ठेवलेल्या दिसतात. हौशी लेखनासाठी वापरता येतील अशा मर्यादित उपलब्ध इमेजेसमधून हव्या तशा इमेजेस मिळाल्या, की पुढची समस्या असते ती त्यांचा आकार, रेझोल्युशन म्हणजे रंग-पोत यांची खोली आणि पार्श्वभूमी म्हणजे बॅकग्राउंड.

सुदैवाने इमेजेसचा मूळ आकार ब्लॉगपोस्टमध्ये बदलणे बर्‍यापैकी सोपे असते. अशा इमेजेस पोस्टमध्ये अडकवताना किंवा नंतरही स्मॉल, मीडियम, लार्ज आणि एक्स्ट्रा लार्ज अशा चार प्रकारात ती रिसाईझ करता येते. तुम्ही HTML कोडमध्ये शिरण्याचे धाडस कराल, तर तुम्हाला अगदी नेमक्या आकारातही ती बसवता येते. निव्वळ मूळ इमेजच्या आकाराच्या प्रमाणातच कमी-जास्त न करता तुमच्या ब्लॉगच्या मांडणी(layout) आणि फॉन्ट यांना सुसंगत असा आकार तुम्हाला ठेवता येतो.

अनेकदा असे होते की चित्राची/रेखाचित्राची पार्श्वभूमी पांढरी असते, किंवा अशा रंगाची असते जो तुमच्या ब्लॉगच्या पार्श्वभूमी म्हणून तुम्ही निवडलेल्या रंगाशी अथवा इमेजशी विसंवादी दिसतो. याने लेखाच्या एकसंधतेला बाधा येते. अशा वेळी, शक्य असेल तर, अशा चित्रांची पार्श्वभूमी 'पारदर्शक' करण्याचा निर्णय मी घेतो. अर्थात मूळ चित्र किती गुंतागुंतीचे आहे यावर हे साध्य होईल की नाही ते अवलंबून असते. असे करण्याचा आणखी एक फायदा असा की भविष्यात तुम्ही आपल्या ब्लॉगची रंगसंगती बदललीत, तर मागे जाऊन या जुन्या पोस्टस्‌मधील इमेजेसची पार्श्वभूमी त्या नव्या रंगाला अनुकूल करत बसण्याची किचकट प्रक्रिया टळते. ही चित्रे, रेखाचित्रे, भाष्यचित्रे नव्या रंगसंगतीशी आपोआप जुळवून घेतात.

काही वेळा फोटोऐवजी एखादा व्हिडिओ तुमच्या लेखनाला चांगला उठाव देऊ शकतो. किंवा लेखनच त्या व्हिडिओबाबत वा फोटोसंदर्भात असू शकते. (’वेचित चाललो...’ या ब्लॉगवर असे बरेच लेखन सापडेल.) मजकूर, फोटो, इमेजेस (ज्यात ग्राफ, रेखाचित्रे वगैरे सारे समाविष्ट होते), ऑडिओ वा व्हिडिओ आणि संदर्भासाठी लिंक्स यांच्या मदतीने तुमचे लेखन अधिक परिपूर्ण करता येते.

(गुगलच्या) ब्लॉगरचा फायदा असा की त्या ब्लॉगवर वापरलेल्या इमेजेस, फोटो हे थेट तुमच्या नावे असलेल्या गुगलच्या फोल्डरमध्ये साठवले जातात. तो फोल्डर तुम्हाला स्वतंत्रपणेही एडिट करता येतो. शिवाय बॅकअप घेताना ब्लॉगर तुमच्या पोस्टसोबत त्या इमेजेसही घेऊन येतो. समजा काही पोस्टस तुम्ही काढून टाकल्या तरी या इमेजेस इथे राहतात. तुम्हाला आवश्यक वाटल्यास त्या थेट गुगलच्या 'ब्लॉगर कंटेंट फोल्डर'मध्ये जाऊन डिलीट करता येतात. उलट दिशेने बर्‍याच इमेज एकदम अपलोड करुन ठेवून भविष्यातील ब्लॉगपोस्ट्समध्ये वापरण्याची सोय करुन ठेवता येते.

दुर्दैवाने व्हिडिओंचे तसे नाही. यू-ट्यूब हे गुगलचेच अपत्य असले तरी व्हिडिओंना जागा अधिक लागते. त्यामुळे जेमतेम १५ जीबी फुकट डेटामध्ये तुमच्या ईमेल, फोटो, डॉक्युमेंट्स, स्प्रेडशीट्स (एक्सेल), प्रेजेंटेशन्स या सार्‍यांसोबत व्हिडिओनी व्यापलेली जागाही मोजली जात असल्याने जागेची चणचण निर्माण होऊ शकते. त्यामुळे व्हिडिओंचा वापर जपूनच करावा लागतो. एक पर्याय म्हणजे अन्य कुणी यू-ट्यूबवर अपलोड केलेला मिळताजुळता व्हिडिओ वापरता येतो. त्याची साठवणुकीची जागा मूळ मालकाच्या कोट्यातून वापरली जात असल्याने आपली बचत होते. पण...

उद्या त्या मालकाने, यू-ट्यूबने वा अन्य कुणी तो डिलीट केला तर लिंक तुटते. यावर उपाय म्हणून असे व्हिडिओ मी माझ्या संगणकावर उतरवून ठेवतो. समजा मूळ ठिकाणाहून तो नाहीसा झाला तर माझ्या कोट्यातून तो नव्याने अपलोड करुन लिंक दुरुस्त करता येते.

आता लेखन पुरे झाल्यानंतरचा पुढचा टप्पा. एका ब्लॉगवर अनेक पोस्ट्स झाल्यानंतर हवी ती शोधणे सुलभ व्हावे, तसेच विषयांनुसार त्यांचे वर्गीकरण करता यावे, त्यांना एकत्र करता यावे, म्हणून प्रत्येक पोस्टला टॅग(tag) किंवा कॅटेगरीज(categories) चिकटवता येतात. उदा. कविता, राजकीय, चित्रपट, संस्कृती वगैरे. त्याचबरोबर पोस्ट ज्या HTML फाईलमध्ये स्टोअर केली जाते, त्याला संदर्भ स्पष्ट करणारे नावही निवडता येते.

साधारणपणे बहुसंख्य ब्लॉगर इथे थांबतात.

(क्रमश:)

पुढील भाग >>माझी ब्लॉगयात्रा - ४ : ब्लॉग लिहिल्यानंतर